AIGC-StableDiffusion

[TOC]

AIGC–Stable Diffusion

Stable Diffusion是一个基于Latent Diffusion Model（LDM）的文转图AI模型，其使用了CLIP ViT-L/14的文本编码器，能够通过文本提示调整图像。它在运行时将成像过程分离成“扩散 （diffusion）”的过程，从有噪声的情况开始，逐渐改善图像，直到完全没有噪声，逐步接近所提供的文本描述。

参考文章：

  1. 在文章写完去学源码时候才找到这两篇文章，写的非常牛逼，非常细节！！文章中许多图、想法来源于它：

    https://zhuanlan.zhihu.com/p/613337342、https://zhuanlan.zhihu.com/p/615310965

  2. 这三篇文章介绍DM模型还有其他内容等非常深入浅出，难以理解的数学公式介绍的非常详细，非常牛逼！！

    https://zhuanlan.zhihu.com/p/637815071、https://zhuanlan.zhihu.com/p/650394311、https://zhuanlan.zhihu.com/p/655568910

  3. 其他文章：

    http://shiyanjun.cn/archives/2212.html、https://jalammar.github.io/illustrated-stable-diffusion/

Latent Diffusion Model文章摘要：

Latent Diffusion Model Abstract

1. 模型结构

结构图：

Stable Diffusion文生图模型简单框架

Stable Diffusion文生图模型框架

模块：

CLIP Text Encoder : 提取输入的text的embedding , 通过 cross attention 方式送入扩散模型的 UNet 中作为 condition，注入语义信息，在训练时以context作为condition，使用cross attention机制来更好的学习文本与图像的匹配关系；

Image Information Creator

  • Image Encoder : 基于 VAE Eecoder 将图像压缩到 latent 空间，用向量表示；

  • UNet+Scheduler : 扩散模型的主体，用来实现文本引导下的 latent 去噪生成；

Image Decode : 根据得到的 Latent Image，基于 VAE Decoder 生成最终的图像。。

过程：

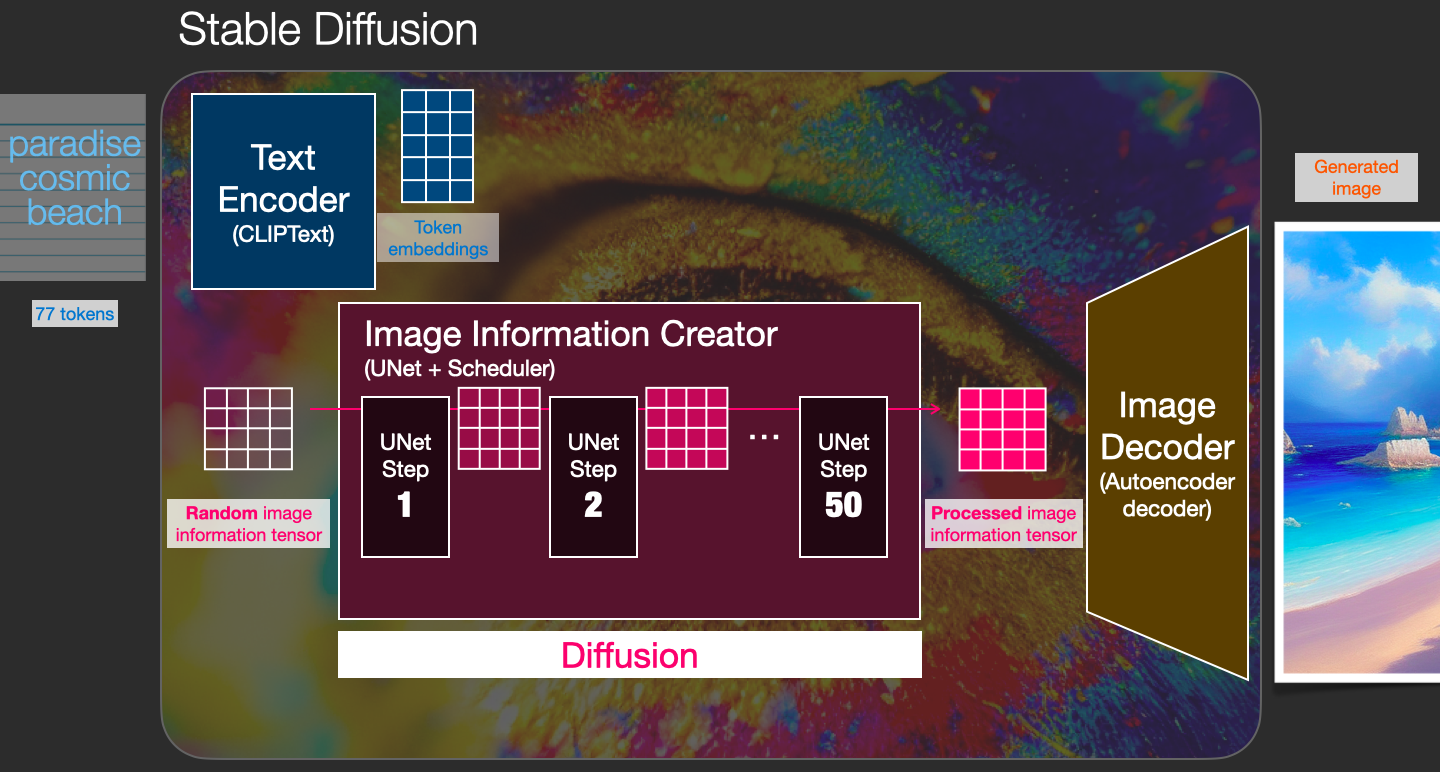
首先，输入 Prompt 提示词 “paradise, cosmic, beach”，经过 CLIP Text Encoder 组件的处理，将输入的 Prompt 提示词转换成 77×768 的 Token Embeddings，该 Embeddings 输入到 Image Information Creator 组件；

这里如果有别的输入信息，比如Semantic Map（语义图）、Text（文本）、Representations（表示）、Images（图像）等，经过不同组件的处理，然后通过 cross attention 方式送入扩散模型的 UNet 中作为 condition。

然后，Random image information tensor 是由一个 Latent Seed（Gaussian noise ~ N(0, 1)） 随机生成的 64×64 大小的图片表示，它表示一个完全的噪声图片，作为 Image Information Creator 组件的另一个初始输入；

接着，通过 Image Information Creator 组件的处理（该过程称为 Diffusion），生成一个包含图片信息的 64×64 的 Latent Image，该输出包含了前面输入 Prompt 提示词所具有的语义信息的图片的信息；

最后，上一步生成的 Latent Image 经过 Image Decoder 组件处理后生成最终的和输入 Prompt 提示词相关的 512×512 大小的图片输出。

2. 具体实现

2.0 到底什么是扩散(Diffusion)？

扩散是发生在“Image Information Creator”组件内部的过程。有了表示输入文本的标记嵌入「Token embeddings」和随机起始图像信息数组「Random image information tensor」，该过程会生成图像解码器用来绘制最终图像的信息数组。

2.1 CLIP Text Encoder

Stable Diffusion所使用的是OpenAI的CLIP的预训练模型的Text Encoder。

2.2 Image Information Creator

2.2.1 Image Encoder「VQ-VAE中的编码器部分」

在Stable Diffusion模型中，Image Encoder（图像编码器）是一个关键组件，用于将图像转换为潜在空间（latent space）中的表示，实现信息的有效压缩和重构。这些表示之后用于生成高质量的图像。

  • 架构

    1. 卷积层：一系列的卷积层，用于逐步提取图像的局部特征。
    2. 池化层：减少特征图的空间维度，从而降低计算复杂度。
    3. 编码层：将提取到的特征转换为潜在向量表示。

  • 工作流程

    1. 输入图像：输入图像首先经过预处理步骤，例如归一化和大小调整。
    2. 卷积层处理：经过多个卷积层和池化层，提取图像的特征并逐步降低空间维度。
    3. 潜在表示生成：通过编码层，将提取的特征转换为潜在空间中的向量表示。

这些潜在向量表示是扩散模型操作的核心，它们在扩散过程中逐步反向扩散（denoising），最终生成高质量的图像。Image Encoder在这个过程中扮演了至关重要的角色，确保输入图像能够被有效地压缩和表示，从而使得扩散过程能够生成准确且高质量的图像。

2.2.2 UNet+Scheduler

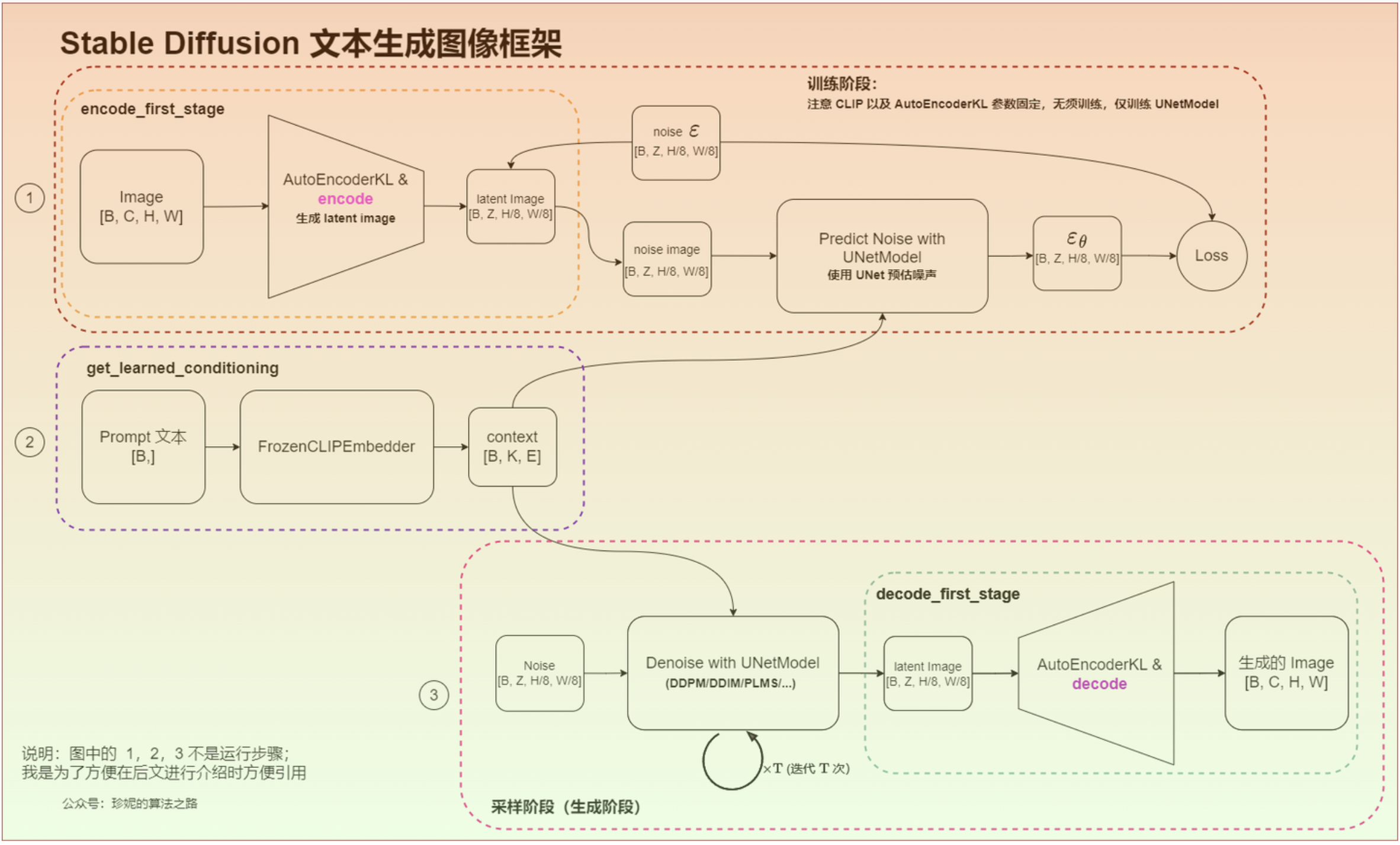
当输入的图像、 文本提示词等信息经过不同组件分别被转换成 Image Embeddings、Token Embeddings… 之后，后续的操作就开始进入 Latent Space 中，通过向量来表示并进行各种处理操作，得到了包含 “原始图像 + 提示词” 信息的图像向量数据信息（Latent Image）。

下图中前向过程（$\varepsilon$为VAE的编码器）是我们生成数据以训练噪声预测器的方式。训练完成后，我们可以通过运行反向过程（$\mathbf{D}$为VAE的解码器）来生成图像。

图2

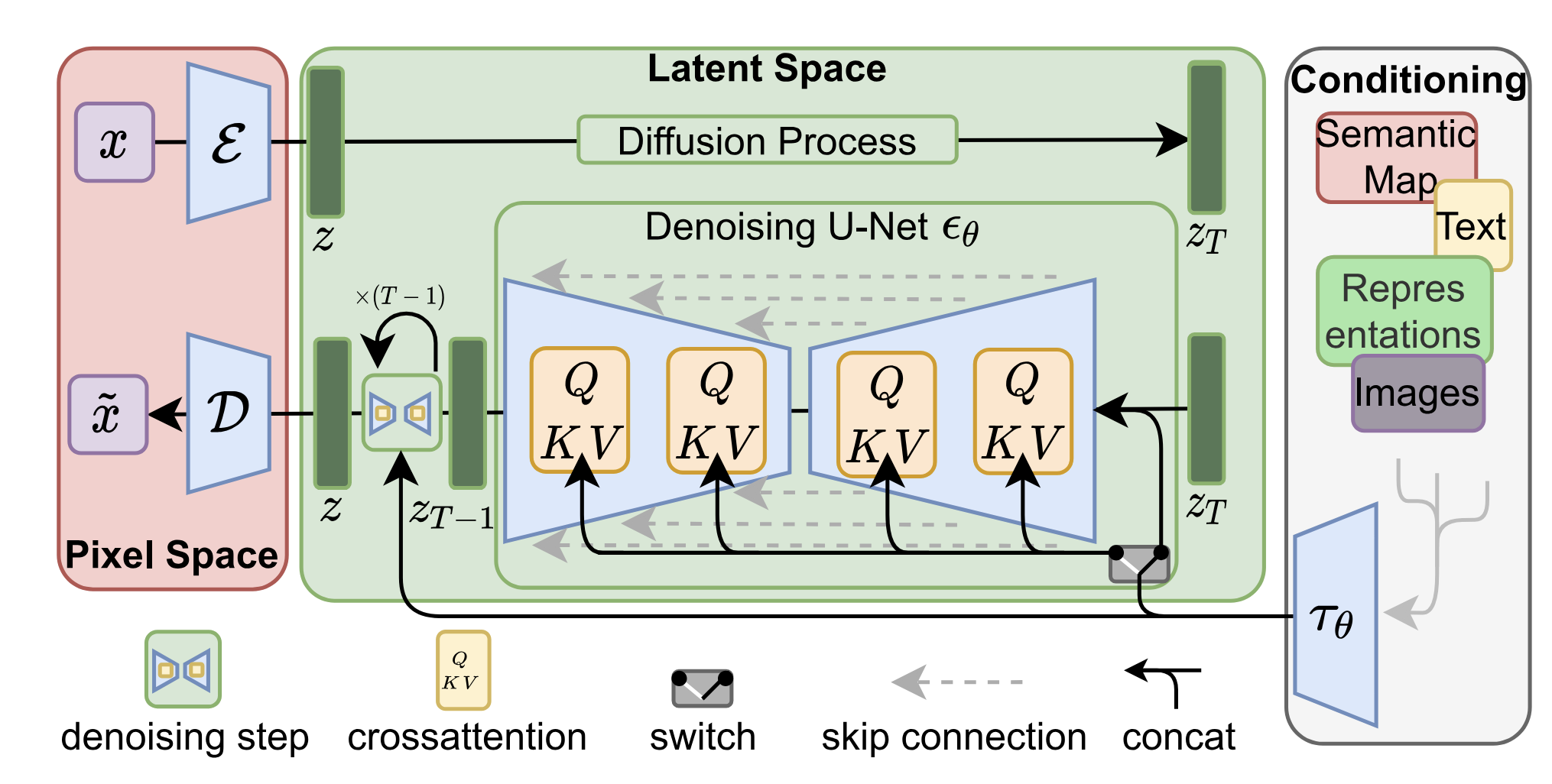
Image Embeddings、Token Embeddings 等是如何在 UNet 网络中整合在一起的：

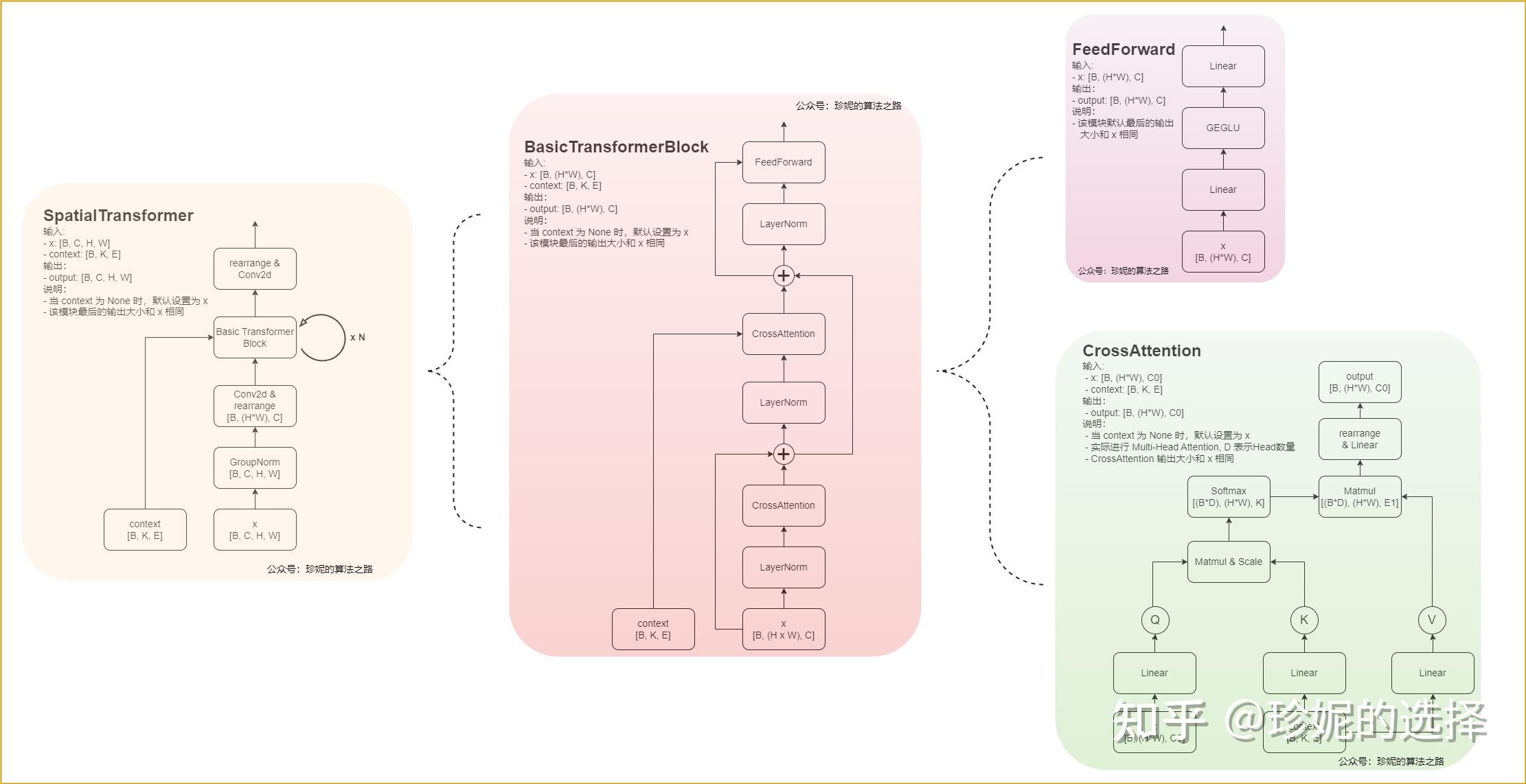
Image Embeddings、Token Embeddings 如何在UNet网络中整合在一起

UNet网络具体结构如下：

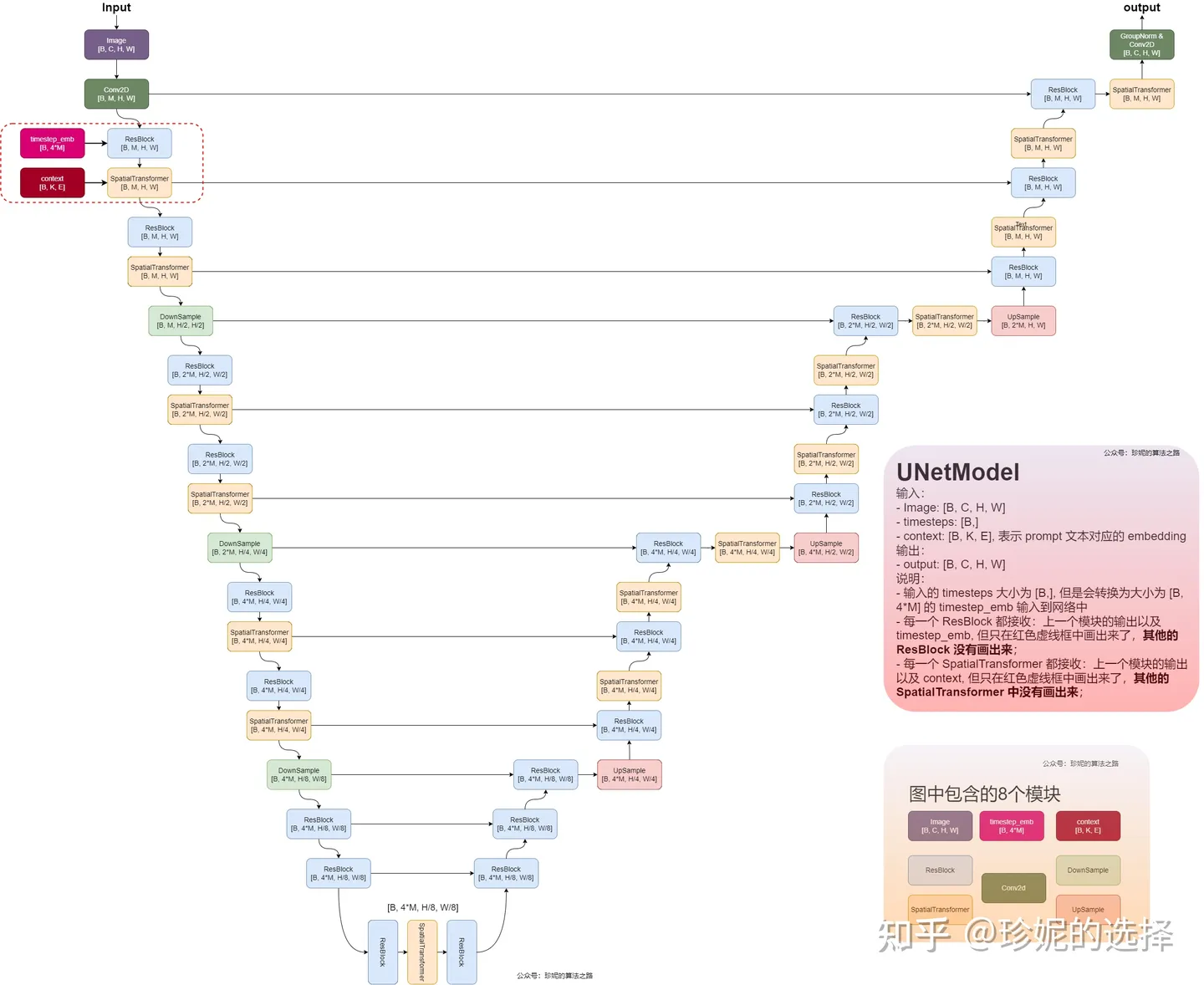
UNet网络

ResBlock+SpatialTransformer具体结构示意图：

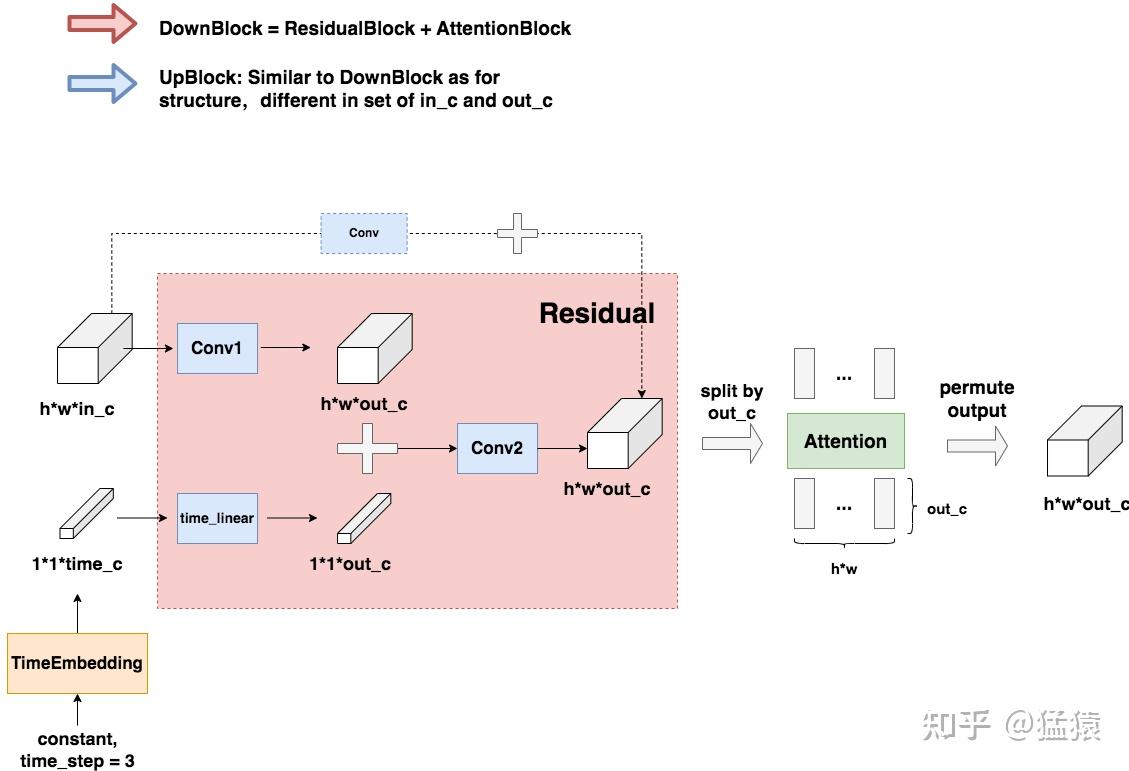
ResBlock+SpatialTransformer

相关组件解释：

  1. time step embedding是由时间步信息编码成的一个高维向量，以便与其他特征进行结合和处理。以下是详细解释：

    这种嵌入方法的目的是将时间步长信息注入到模型中，使模型能够在生成过程中考虑时间维度上的变化。这种方法在稳定扩散模型中非常重要，因为它能够帮助模型在每个时间步长上进行准确的预测和生成。

    生成 timestep_embedding 的方法如下：

    1. Sine 和 Cosine 位置编码：

      这种方法类似于 Transformer 模型中使用的位置编码。它使用正弦和余弦函数将时间步长嵌入到一个高维空间中。具体步骤如下：对每个时间步长 ( t ) 生成一个向量，其中每个维度对应一个特定的频率。使用正弦和余弦函数对这些频率进行编码。

      具体公式如下：其中( t ) 是时间步长；( i ) 是向量的维度索引；( d ) 是向量的维度。

      $\text{PE}_{(t, 2i)} = \sin \left( \frac{t}{10000^{2i/d}} \right) $

      $\text{PE}_{(t, 2i+1)} = \cos \left( \frac{t}{10000^{2i/d}} \right) $

    2. 线性变换：
      生成的正弦和余弦位置编码向量通常会通过一个线性变换层，以适应模型的输入维度。

    3. 结合噪声预测：
      在噪声预测模型中，时间步长嵌入有助于模型理解不同时间步长下的噪声分布，从而更好地进行预测和生成。

2.3 Image Decoder「VQ-VAE中的解码器部分」

最后要把这个Latent Image，基于 VAE Decoder 从 Latent Space 再映射到 Pixel Space，得到我们最终需要生成的视觉图像。

3. DDPM、DDIM、PLMS

3.1 DDPM (denoising diffusion probabilistic models)

在上面所说的几个博客中已经介绍的非常详细了，而且其中的数学公式在大牛的博客中介绍的也非常详细了，但是推导过程依然有些懵懂，常看常新叭。主要解释了以下几个问题：

  1. 最大似然估计

    最大似然估计（Maximum Likelihood Estimation, MLE）是一种统计方法，用于估计模型参数，使得在给定观察数据的情况下，模型生成这些数据的概率最大。简单来说，MLE 通过最大化似然函数来找到最符合已知数据的模型参数。

    基本思想:

    假设我们有一个数据集 ${x_1, x_2, …, x_m}$，这些数据点是从某个概率分布 $P_{\text{data}}(x)$中抽取出来的。我们想要用一个参数化的模型 $P_\theta(x)$来近似这个分布，其中 ( $\theta$ ) 是模型的参数。

    最大似然估计的目标函数是对数似然函数的和，即：$\sum_{i=1}^{m} \log P_\theta(x_i) $

    在DDPM中公式推导步骤:

    最小化KL散度

    第一步：$[ \arg\max_\theta \int P_{\text{data}}(x) \log P_\theta(x) , dx ]$，这个积分表示在整个数据分布上的对数似然函数「$\log P_{\theta}(x)$」的期望。

    第二步：$[\arg\max_\theta E_{x \sim P_{\text{data}}}[\log P_\theta(x)]]$，利用期望的定义，我们可以把积分表示成期望的形式。

    这里， $( E_{x \sim P_{\text{data}}} )$ 表示根据数据分布 $( P_{\text{data}}(x) )$ 的期望。

    第三步：$[ \arg\max_\theta \sum_{i=1}^{m} \log P_\theta(x_i) ]$，在实际操作中，我们没有 $P_{\text{data}} $ 的精确形式，而是只有一个有限的数据样本 ${x_1, x_2, …, x_m}$。因此，我们使用样本均值来近似期望，这一步的近似就是在数据样本上的对数似然的求和。通过最大化这个和，我们就可以找到最符合数据的模型参数 $( \theta )$。

  2. ELBO「Evidence Lower Bound」

    $argmax_{\theta}\prod_{i=1}^{m}P_\theta(x_i)$ 的本质就是要使得连乘中的每一项最大，也等同于使得$\log P_{\theta}(x)$最大。所以我们进一步来拆解 。

    ELBO

  3. 重参数「Reparamterization」技术

    之前想得到t时刻的加噪图像，需要：$q(x_t|x_{t-1})$；通过重参数技术：$q(x_t|x_0)$

    具体来说，在重参数的表达下，第t个时刻的输入图片可以表示为：$x_t = \sqrt{\bar{\alpha_t}}x_0+\sqrt{1-\bar{\alpha_t}}\epsilon$

    也就是说，我们每次只需要对符合高斯分布的噪声 $\epsilon$ 采样，就能得到 t 时刻的加噪图

    “从一个带参数的分布中进行采样”转变到“从一个确定的分布中进行采样”，解决了梯度无法传递的问题。

DDPM、DDIM、和PLMS都是扩散模型（Diffusion Models）相关的概念，主要用于图像生成任务。它们都是通过逐步去噪（denoising）的过程来生成数据，但具体的去噪过程和方法有所不同。以下是对这三种方法的简要解释及其区别：

3.2 DDPM、DDIM、PLMS 有什么区别

1. DDPM（Denoising Diffusion Probabilistic Models）

基本原理：

DDPM是扩散模型的原始形式之一，通过一个逐步加噪（forward process）和去噪（reverse process）的过程来生成数据。

加噪过程（Forward Process）：从真实数据分布开始，逐步加入噪声，生成一系列中间状态直至完全噪声化。这个过程通常被定义为一个马尔可夫链。

去噪过程（Reverse Process）：从完全噪声的状态开始，逐步去噪恢复到原始数据分布。这个过程通过训练一个神经网络模型来近似实现，每一步预测并去除一小部分噪声。

特点：

  • DDPM的去噪过程通过多个小步骤进行，每一步都需要一个神经网络的前向传递。

  • 通常需要非常多的时间步（上千步）来生成高质量图像，这导致生成过程较慢。

2. DDIM（Denoising Diffusion Implicit Models）

基本原理：

DDIM是一种基于DDPM的改进，旨在加速生成过程。它提出了一种非马尔可夫链的去噪过程，并保持了与原始数据分布的相似性。

非马尔可夫去噪：与DDPM的马尔可夫链不同，DDIM使用一种非马尔可夫链去噪方法，允许跳过中间的多个时间步，从而加快生成速度。

特点：

DDIM在减少生成步骤的同时，可以保持生成图像的质量。

它提供了一种显式的去噪解，这意味着可以直接计算出从噪声到数据的映射，而不依赖于逐步迭代。

通常比DDPM更快，因为需要的去噪步骤更少（几十步到几百步）。

3. PLMS（Pseudo Linear Multistep Scheme）

基本原理：

PLMS是一种基于DDPM和DDIM的改进方法，进一步减少生成步骤。它使用一种伪线性多步方法来预测去噪过程中的多个步骤。

多步方法：PLMS使用一个多步预测方法，这种方法在每一步中利用之前几个时间步的预测结果来提高当前的预测精度。

特点：

PLMS进一步加快了生成过程，比DDIM需要更少的去噪步骤。

它通过使用多步历史信息来提高去噪过程的稳定性和精度。

在实际应用中，PLMS通常能够在保持生成质量的前提下显著减少生成步骤数，达到类似于DDIM甚至更好的生成效果。

4. 总结

DDPM 是最原始的去噪扩散模型，需要逐步还原图像，步骤多且慢。

DDIM 提供了一种非马尔可夫的去噪方法，可以跳过一些步骤，加速生成过程。

PLMS 在DDIM的基础上，通过多步预测进一步减少生成步骤，并提高生成效率。

4. 补充知识

4.1 VQ-VAE（Vector Quantized Variational Autoencoder）

关于 VQ-VAE「Vector Quantized Variational Autoencoder，VQ-VAE」，是一种将离散表示学习引入自编码器框架的模型。它结合了传统变分自编码器（VAE）和向量量化技术，使模型能够在离散的潜在空间中进行编码和解码。这张图描述了向量量化变分自编码器的工作原理:

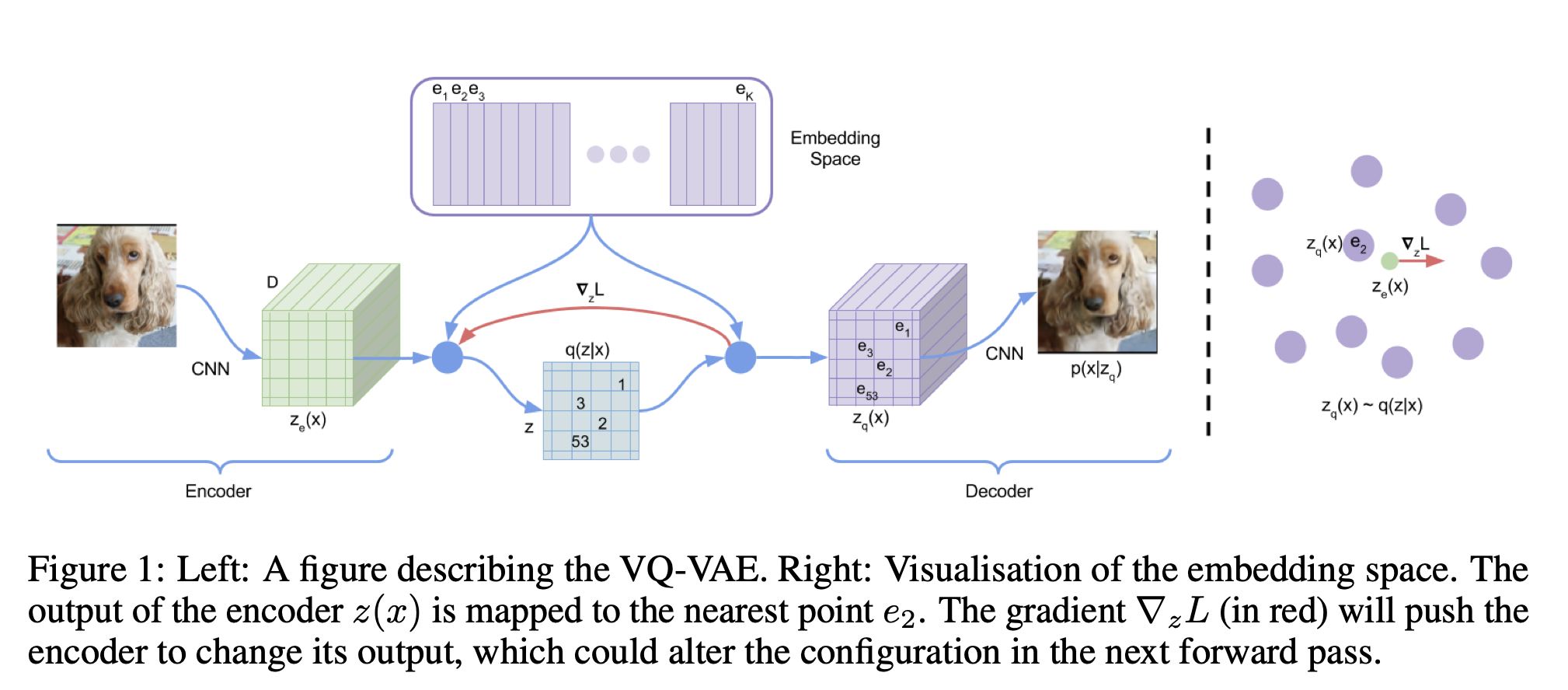
VQ-VAE

左侧部分：

  • 输入图像：首先输入的是一张狗的图像。
  • 编码器（Encoder）：输入图像经过卷积神经网络（CNN）编码器，生成编码表示$ z_e(x) $。
  • 离散化（Discretization）：编码表示$z_e(x) $被映射到最近的嵌入点$ e_2 $，形成离散表示$z_q(x) $。
  • 量化（Quantization）：离散表示$z_q(x)$通过查找表将编码表示映射到最近的嵌入向量，形成量化表示。

右侧部分:

  • 嵌入空间（Embedding Space）：展示了嵌入空间的可视化。在这个空间中，编码器输出$ z_e(x) $被映射到最近的嵌入点$e_2$。
  • 梯度更新（Gradient Update）：红色箭头表示梯度$\nabla_{z}L$的方向，嵌入空间中的点通过梯度更新，推动编码器改变输出，从而优化整个模型。

其中，Encoder 能够将一个图像压缩到低维空间表示，在 Stable Diffusion 模型中，将原始输入图像通过 Encode 转换成 Latent Space 中的向量表示 Latent Image；

Decoder 能够将一个压缩表示的图像向量数据转换成高维空间表示，在 Stable Diffusion 模型中将 Latent Space 中图像的向量表示 Latent Image 通过 Decode 转换成 Pixel Space 中的视觉图像。

其中一些概念：

  1. 连续表示（Continuous Representation）

    输入数据：假设输入数据 x 是一张图像。

    编码器（Encoder）：编码器 E 是一个神经网络，通常由多个卷积层组成。它将输入图像 x 映射到一个连续的在表示 $z_e = E(x)$，这里， $z_e$ 是一个连续值的向量，表示图像的特征。

  2. 向量表示（Vector Representation）

    码本（Codebook）：码本 e 是一个固定大小的向量集合，记为 ${e_1, e_2, \ldots, e_K}$ ，其中 K 是码本向量的数量。每个向量 $e_i$ 通常是随机初始化的，并在训练过程中更新。

  3. 量化表示（Quantized Representation）

    向量量化（Vector Quantization）：向量量化的目的是将连续的潜在表示 $z_e$ 映射到离散的码本向量 $ e_i $。具体来说，对于每个 $z_e$ ，找到与其最接近的码本向量 $ e_i $，并用 $e_i $ 代替 $ z_e $。

    量化过程如下：$z_q = \text{argmin}_{e_i} | z_e - e_i |$，这里，$ z_q $ 是量化后的离散潜在表示，它与最近的码本向量 $e_i$相等。

  4. 解码过程（Decoding Process）

    解码器（Decoder）：解码器 D 将量化后的离散潜在表示 z_q 映射回输入数据空间，重建输入图像：$\hat{x} = D(z_q)$，这里， $\hat{x}$ 是解码器生成的重建图像。

损失函数（Loss Function）:

VQ-VAE 的损失函数由三部分组成：

  1. 重构损失（Reconstruction Loss）：衡量原始输入 x 和重建输出 $ \hat{x}$ 之间的差异，通常使用均方误差（MSE）。
    $$
    \mathcal{L}_{\text{recon}} = | x - \hat{x} |^2
    $$

  2. 向量量化损失（Vector Quantization Loss）：鼓励码本向量 $e_i $ 接近连续潜在表示 $z_e $
    $$
    \mathcal{L}_{\text{vq}} = | \text{sg}[z_e] - e_i |^2
    $$
    其中，$\text{sg}$ 表示停止梯度（stop gradient），即在反向传播时不计算其梯度。

  3. 承诺损失（Commitment Loss）：鼓励连续潜在表示 $z_e$ 稳定，以减少解码器的训练难度。
    $$
    \mathcal{L}_{\text{commit}} = \beta | z_e - \text{sg}[e_i] |
    $$
    其中，$\beta$ 是超参数，控制承诺损失的权重。

  4. 总损失函数是上述三部分损失的加权和：

$$
\mathcal{L} = \mathcal{L}{\text{recon}} + \mathcal{L}{\text{vq}} + \mathcal{L}_{\text{commit}}
$$

4.2 什么叫做转换为潜在空间中的向量表示，它和提取的图像特征不是一回事吗？

将图像转换为潜在空间中的向量表示是特征提取的进一步抽象和压缩过程。这一过程的主要目的是将高维的、冗长的特征图压缩为低维的紧凑表示，同时保留图像的核心信息，便于后续的生成和操作。

  • 图像特征提取

    图像特征提取是指从输入图像中提取出能够代表图像内容的重要信息。这通常是通过一系列的卷积操作和其他神经网络层来实现的。特征提取的主要目标是捕捉图像的局部和全局信息，包括颜色、纹理、形状等。

  • 潜在空间中的向量表示

    潜在空间中的向量表示是通过对图像特征进一步处理得到的。这些表示通常是低维的紧凑向量，包含了图像的高层次抽象信息。潜在空间中的向量表示的主要目的是将图像数据压缩到一个更易处理和操作的形式，同时保留图像的关键信息。

  • 例子

    假设我们有一张猫的图像：

    1. 特征提取：卷积神经网络提取出猫的边缘、纹理、耳朵形状等特征，形成一个高维的特征图。
    2. 潜在表示：特征图通过编码器压缩为一个低维向量。这个向量可能表示为[0.8, -1.2, 0.3, …]，其中的每个值都对应着图像的一些高层次特征，例如猫的种类、颜色、姿态等。

4.3 时间步骤（timestep）和条件信息（context embedding）

在 Stable Diffusion 模型中，时间步骤（timestep）和条件信息（如文本嵌入）被注入到不同的网络组件中，这是为了最大化它们在生成过程中的作用和效率。

  • 时间步骤加入到 ResBlock:

时间步骤通常通过时间嵌入的形式加入到残差块（ResBlock）中。通俗点来说，由于模型每一步的去噪都用的是同一个模型，所以我们必须告诉模型，现在进行的是哪一步去噪。因此我们要引入timestep，允许模型在每一层都根据当前的时间步骤调整其处理方式。timestep的表达方法类似于Transformer中的位置编码，将一个常数转换为一个向量，再和我们的输入图片进行相加。

  • 条件信息加入到 Spatial Transformer:

条件信息，如文本嵌入，通常通过空间变换器（Spatial Transformer），也就是交叉注意力机制，加入到模型中。Spatial Transformer允许模型在图像特征和条件信息之间建立复杂的对应关系。通过使用交叉注意力，模型可以根据图像的每个部分和条件信息之间的关系来动态调整图像特征。这种方式特别适合处理与空间位置相关的信息，因为它可以让模型关注条件信息中与当前正在生成的图像区域最相关的部分。

二段式检测算法和一段式的区别

NMS的流程

OCR

Clip 文本和图像LOSS

BERT masked Masked作用在哪 还有在transformer中的masked

stablediffusion ldm

embedings以交叉注意力的方式注入是什么意思？ -> QKV

botsort 卡尔曼滤波升级在哪 和sort deepsort升级在哪

算法：最长不重复子序列的长度 -> 滑动窗口+哈希表

Deep Learning > AIGC
#Stable Diffusion
AIGC-StableDiffusion
https://adzuki23.github.io/2024/06/28/AIGC-StableDiffusion/
作者
Hongyu Li
发布于
2024年6月28日
更新于
2024年8月3日
许可协议