LeetCode

LeetCode 热题100

[TOC]

Hashtable

1. 1:两数之和

# Hash表 # 数组

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

解决：

暴力枚举法空间复杂度$O(1)$ 时间复杂度$O(N^2)$

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        n = len(nums)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[i] + nums[j] == target:
                    return [i, j]        
        return []

Hash法空间复杂度$O(N)$ 时间复杂度$O(N)$

class Solution(object):
   def twoSum(self, nums: List[int], target: int):
       hashtable = dict()
       for i, num in enumerate(nums):
           if target - num in hashtable:
               return [hashtable[target-num], i]
           hashtable[nums[i]] = i
       return []

总结：

enumerate()是python的内置函数，用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。

1
2
3

enumerate(sequence, [start=0])
* sequence: 一个序列、迭代器或其他支持迭代对象。
* start: 下标起始位置。

seasons = ['Spring', 'Summer', 'Fall', 'Winter']

list(enumerate(seasons))
[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
list(enumerate(seasons, start=1))       # 下标从 1 开始
[(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]

2. 149:字母异位词分组

# Hash表 # 数组 # 字符串

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

解决：

Hash表时间复杂度$O(nk\log{k})$ 空间复杂度$O(nk)$

其中 n 是 strs 中的字符串的数量，k 是 strs 中的字符串的的最大长度。

class Solution(object):
    def groupAnagrams(self, strs: List[str]):
        hashtable = collections.defaultdict(list)
        for s in strs:
            key = "".join(sorted(s))
            hashtable[key].append(s)
        return list(hashtable.values())

计数时间复杂度$O(n(k+26)$ 空间复杂度$O(n(k+26))$

class Solution(object):
    def groupAnagrams(self, strs):
        hashtable = collections.defaultdict(list)
        for s in strs:
            count = [0] * 26
            for c in s:
                count[ord(c)-ord("a")] += 1
            hashtable[tuple(count)].append(s)
        return list(hashtable.values())

总结：

在这里使用hashtable={}可能会有一些keyError等问题，需要我们多写一些代码，而使用defaultdict可以避免：

defaultdict 的构造函数接受一个工厂函数作为参数，这个工厂函数在访问不存在的键时会被调用生成默认值。例如，defaultdict(list) 表示当访问的键不存在时，会自动生成一个空列表作为默认值。
Map、HashTable、Dict等的区别和联系

3. 128:最长连续序列

# Hash表 # 数组

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

解决：

数组排序时间复杂度$O(n\log{n})$ 空间复杂度$O(1)$

class Solution(object):
    def longestConsecutive(self, nums: List[int])->int:
        if nums == []:
            return 0
        nums_sorted = sorted(nums)
        max_length = 1
        tmp = 1
        for i in range(len(nums_sorted) - 1):
            if nums_sorted[i+1] == nums_sorted[i]+1:
                tmp += 1
            elif nums_sorted[i+1] == nums_sorted[i]:
                continue
            else:
                tmp=1
            if tmp>max_length:
                max_length = tmp
        return max_length

Hash表时间复杂度$O(N)$ 空间复杂度$O(N)$

class Solution(object):
    def longestConsecutive(self, nums):
        nums_set = set(nums)
        longest_streak = 0
				
        # 非常聪明的将时间复杂度高的‘排序’替换为‘查找’
        for n in nums_set:
            if n-1 not in nums_set:
                current_num = n
                current_streak = 1

                while current_num+1 in nums_set:
                    current_num += 1
                    current_streak += 1
                
                longest_streak = max(current_streak, longest_streak)
        return longest_streak

总结：

在Python中，set() 是一种数据结构，用于存储不重复的元素集合。

集合（set）是一种无序的数据结构，不支持通过索引来访问元素。集合中的元素是无序的，因此没有像列表那样的索引机制。

集合（Set）在底层是通过哈希表实现的。哈希表通过哈希函数将元素映射到一个存储桶，理论上可以在常数时间内完成插入、删除和查找操作。因此，查找一个元素是否在集合中，平均时间复杂度是 O(1)。

列表（List）

列表（List）是一个有序集合，元素按顺序存储。为了查找一个元素是否在列表中，最坏情况下需要遍历整个列表，检查每个元素。因此，查找操作的时间复杂度是 O(n)，其中 n 是列表中的元素数量。

双指针

4. 283:移动零

# 数组 # 双指针

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

解决：

双指针时间复杂度$O(N)$ 空间复杂度$O(1)$

class Solution(object):
    def moveZeroes(self, nums):
        left = right = 0
        num_len = len(nums) 
				# right指针遍历整个列表
        while right < num_len:
          	# right指针的目标就是寻找非零值与left指针交换，当找到则两个指针同时右移
            if nums[right] != 0:
                nums[left], nums[right] = nums[right], nums[left]
                left += 1
            right += 1

总结：

这道题的难度被归为简单，解决方法标签为双指针。但是我很疑惑python中如何实现C++中传统的指针功能，ChatGPT回答如下：

在 Python 中，虽然没有直接的指针概念，但你可以通过几种方式实现类似于 C++ 中指针的功能。主要方法包括使用对象的引用、可变数据类型以及通过封装类来模拟指针行为。
1.在 Python 中，所有变量实际上都是对象的引用（类似于指针）。通过传递对象的引用，可以实现类似指针的功能。
2.Python 的可变数据类型（如列表、字典和自定义对象）可以用于模拟指针的行为，因为它们可以在函数调用中被修改。
3....

这道题其实还有一些解决办法，比如找到0后面的数都往前移动、或者暴力对列表remove/append等，但是时间复杂度会很高。

这个双指针的解决办法说实话很巧妙，但是理解起来有点复杂，评论区说可以按快排的原理去理解，在这里梳理一下：
- 当L和R指针指向同一个位置的时候，此时还没有遇到0，交换位置无所谓；
- 当L和R指针不指向同一个位置的时候，就一定是遇到了0，此后，L指针一定是指向0，它的左边是处理好的数据。

5. 11:盛最多水的容器

# 贪心 # 双指针 # 数组

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

说明：你不能倾斜容器。

解决：

双指针时间复杂度$O(N)$ 空间复杂度$O(1)$

class Solution(object):
    def maxArea(self, height):
        lens = len(height)
        left = 0
        right = lens-1

        maxArea = 0
        curArea = 0
        
        while left != right:
            if height[left] <= height[right]:
                curArea = height[left] * (right-left)
                left += 1
            else:
                curArea = height[right] * (right-left)
                right -=1
            
            maxArea = max(maxArea,curArea)
        return maxArea

总结：

这道题也可以用暴力解法，双层循环遍历两次列表，判断每一组值，但是时间复杂度为$O(N^2)$。
一开始两个指针一个指向开头一个指向结尾，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，这种情况下我们想要让指针移动后的容器面积增大，就要使移动后的容器的高尽量大，所以我们选择指针所指的高较小的那个指针进行移动，这样我们就保留了容器较高的那条边，放弃了较小的那条边，以获得有更高的边的机会。

6. 15:三数之和

# 排序 # 双指针 # 数组

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

解决：

双指针时间复杂度$O(N^2)$ 空间复杂度$O(1)$

class Solution(object):
    def threeSum(self, nums):
        nums_sort = sorted(nums)
        res = []
        for i in range(len(nums_sort)):
            if nums_sort[i] > 0:
                break
            # 去重
            if i > 0 and nums_sort[i] == nums_sort[i-1]:
                continue
            # 双指针
            l = i+1
            r = len(nums_sort)-1
            while l < r:
                s = nums_sort[l] + nums_sort[r] + nums_sort[i]
                if s == 0:
                    res.append([nums_sort[i],nums_sort[l],nums_sort[r]])
                    r -= 1
                    # 去重
                    while l<r and nums_sort[r]== nums_sort[r+1]:r -= 1
                    l += 1
                    # 去重
                    while l<r and nums_sort[l]== nums_sort[l-1]:l += 1
                elif s > 0:
                    r -= 1
                    # 去重
                    while l<r and nums_sort[r]== nums_sort[r+1]:r -= 1 
                elif s < 0:
                    l += 1
                    # 去重
                    while l<r and nums_sort[l]== nums_sort[l-1]:l += 1
        return res

总结：

双指针解法中 l = i+1 而不是 l = 0 的原因是，如果每次从0开始会造成重复解，for循环遍历每个数，与每个数有关的解都已经被列出，遍历到其他数时，不应该再包含之前已经处理好的值。
为什么不能用set方法先直接去掉重复的数字？因为像[-1,-1,2]这样的例子就不可行。

7. 42:接雨水

# 栈 # 数组 # 双指针 # 动态规划 #单调栈

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

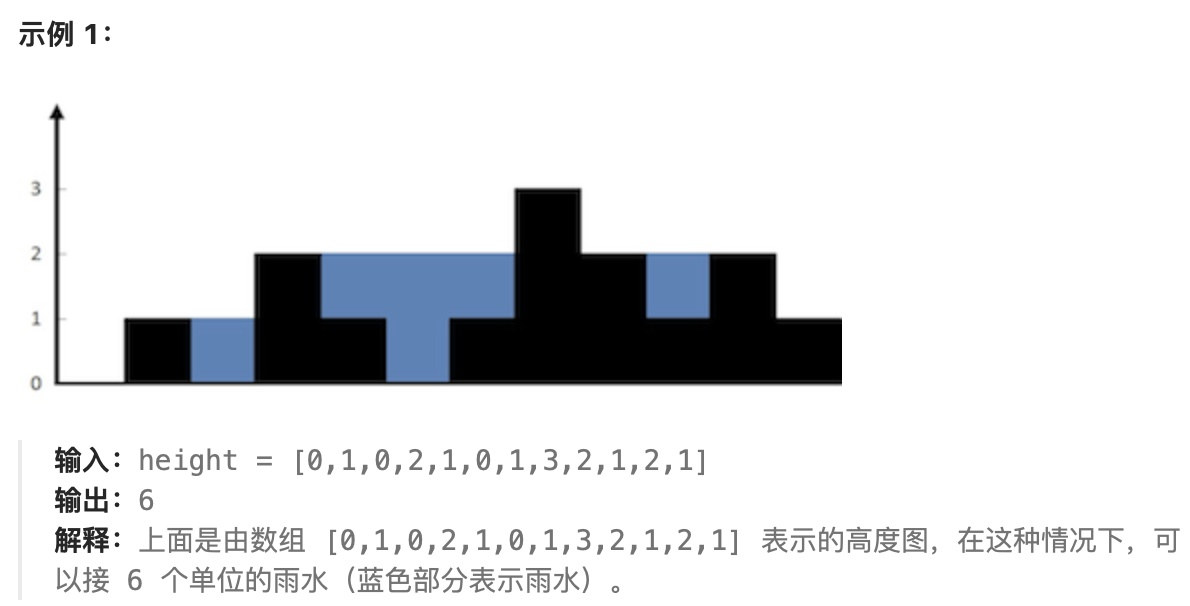
接雨水示例1

解决：

动态规划「按列」时间复杂度$O(N)$ 空间复杂度$O(N)$

对于下标 i，下雨后水能到达的最大高度等于下标i两边的最大高度的最小值，下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。

'''
朴素的做法是对于数组 height 中的每个元素，分别向左和向右扫描并记录左边和右边的最大高度，然后计算每个下标位置能接的雨水量。该做法需要对每个下标位置使用 O(n) 的时间向两边扫描并得到最大高度，因此总时间复杂度是 O(n^2)。
使用动态规划的方法，可以在 O(n) 的时间内预处理得到每个位置两边的最大高度:
leftMax[i] = max(leftMax[i-1], height[i])
rightMax[i] = max(rightMax[i+1], height[i])
'''
class Solution(object):
    def trap(self, height):
        n = len(height)
        ans = 0
        leftMax = [height[0]] + [0] * (n-1)
        for i in range(1, n):
            leftMax[i] = max(leftMax[i-1], height[i])

        rightMax = [0] * (n-1) + [height[n-1]]
        for i in range(n-2, -1, -1):
            rightMax[i] = max(rightMax[i+1], height[i])
        
        for i in range(n):
            ans += min(leftMax[i], rightMax[i]) - height[i]
        
        return ans

单调栈「按行」时间复杂度$O(N)$ 空间复杂度$O(N)$

维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下标对应的数组 height 中的元素递减。

'''
1. 从左到右遍历数组，遍历到下标 i 时，如果栈内至少有两个元素，记栈顶元素为 top，top 的下面一个元素是 left，则一定有 height[left]≥height[top]。如果height[i]>height[top]，则得到一个可以接雨水的区域，该区域的宽度是i−left−1，高度是min(height[left],height[i])−height[top]，根据宽度和高度即可计算得到该区域能接的雨水量。
2. 为了得到 left，需要将 top 出栈。在对 top 计算能接的雨水量之后，left 变成新的 top，重复上述操作，直到栈变为空，或者栈顶下标对应的 height 中的元素大于或等于 height[i]。
3. 在对下标 i 处计算能接的雨水量之后，将 i 入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
'''
class Solution(object):
    def trap(self, height):
        ans = 0
        stack = list()
        n = len(height)

        for i, h in enumerate (height):
            while stack and h > height[stack[-1]]:
                top = stack.pop()
                # 左边界构不成存储雨水的条件，直接退出
                if not stack:
                    break
                # 构成存储雨水的条件
                left = stack[-1]
                curWidth = i - left - 1
                curHeight = min(height[left], height[i]) - height[top]
                ans += curWidth * curHeight
            stack.append(i)
        return ans

双指针「按列」 时间复杂度$O(N)$ 空间复杂度$O(1)$

解决动态规划的空间复杂度问题

class Solution(object):
    def trap(self, height):
        ans = 0
        n = len(height)
        l = 0
        r = n-1
        lmax = rmax = 0
        while l < r:
            lmax = max(lmax, height[l])
            rmax = max(rmax, height[r])
            if height[l]<height[r]:
                ans += lmax - height[l]
                l += 1
            else:
                ans += rmax - height[r]
                r -= 1
        return ans

总结：

这里最简单的就是第三种-双指针解法，用左右指针lmax、rmax分别指向当前位置左边和右边最大的值，非常简单高效。

滑动窗口

8. 3: 无重复字符的最长字串

# 滑动窗口 # Hash表

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

解决：

滑动窗口法：

class Solution(object):
    def lengthOfLongestSubstring(self, s):
        s_dict = set()
        n = len(s)
        maxlength = curlength = 0
        left = 0
        for i in range(n):
            curlength += 1
            while s[i] in s_dict:
                s_dict.remove(s[left])
                left += 1
                curlength -= 1
            if curlength > maxlength:
                maxlength = curlength
                longest_s = s[left:i+1]
            s_dict.add(s[i])
        return maxlength

总结：

最笨的方法是双层遍历，每个字符我都计算以它开头的最长无重复字串的长度，但是这样不聪明，如下所示：
把问题进行延伸，我不仅想要知道长度，还想知道这个字串是什么。我本来以为要用一个队列来实现，后来发现，在我们更改maxLength时候，left指向的就是最长队列的开头，i指向的就是最长队列的末尾，此时进行记录即可。

9. 438: 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

解决：

暴力循环时间复杂度$O(n\log n)$ 空间复杂度$O(1)$

class Solution(object):
    def findAnagrams(self, s, p):
        p_sorted = ''.join(sorted(p))
        n_s = len(s)
        n_p = len(p)
        index=[]
        for i in range(n_s-n_p+1):
            s_i = s[i:i+n_p]
            s_sorted = ''.join(sorted(s_i))
            if s_sorted == p_sorted:
                index.append(i)
        return index

滑动窗口

class Solution(object):
    def findAnagrams(self, s, p):
        n_s = len(s)
        n_p = len(p)

        if n_s < n_p:
            return []

        # 使用数组来存储字符串 p 和滑动窗口中每种字母的数量
        count_s = [0] * 26
        count_p = [0] * 26
        ans = []
    
        for i in range(n_p):
            count_p[ord(p[i])-ord('a')] += 1
            count_s[ord(s[i])-ord('a')] += 1

        if count_s == count_p:
            ans.append(0)

        for i in range(n_s - n_p):
            count_s[ord(s[i]) - ord('a')] -= 1
            count_s[ord(s[i + n_p]) - ord('a')] += 1
            if count_s == count_p:
                ans.append(i+1)
        
        return ans

总结：

这道题用滑动窗口解法，动态的维持当前窗口内每种字母的值，替代了将字符进行排序的方法，减少了时间复杂度。

字串

10. 560: 和为 K 的子数组

# 数组 # 哈希表 # 前缀和

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。

子数组是数组中元素的连续非空序列。

这个题很有意思的是看评论区很多人直觉用滑动窗口做，结果没有考虑数组中有负数的情况，有负数意味着left向右/right向右移动不一定会造成sum的减小/增大。

解决：

枚举法时间复杂度$O(N^2)$ 空间复杂度$O(1)$

class Solution(object):
    def subarraySum(self, nums, k):
        count = 0
        for i in range(len(nums)):
            sum = 0
            for j in range(i,-1,-1):
                sum += nums[j]
                if sum == k:
                    count += 1
        return count

前缀和

from collections import defaultdict

def subarraySum(nums:list[int], k:int)->int:
    # 当前前缀和=0
    s = 0
    # 返回值：统计子数组等于k的次数
    ans = 0
    # mp：[前缀和:出现的次数]
    mp = defaultdict(int)
    # mp[0]=1：是为了处理当前前缀和 s=k 的情况
    mp[0] = 1

    for n in nums:
        # 计算当前的前缀和
        s += n
        if s-target in mp:
            ans += mp[s-target]
        mp[s] += 1
    return ans

11. 239: 滑动窗口最大值

#队列 #数组 #滑动窗口 #单调队列 #堆（优先队列）

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

解决：

优先队列

import heapq
def maxSlidingWindow(nums: list[int], k: int) -> list[int]:
    q = [(-nums[i],i) for i in range(k)]
    heapq.heapify(q)
    max_num = -q[0][0]
    ans = [max_num]
    
    for i in range(k,len(nums)):
        heapq.heappush(q, (-nums[i],i))
        while q[0][1] < i-k:
            heapq.heappop(q)
        ans.append(-q[0][0])
    return ans

单调队列

from collections import deque
def maxSlidingWindow(nums: list[int], k: int) -> list[int]:
    ans = []
    q = deque()
   
    # 这里是第一个滑动窗口
    # 依次将下标加入到队列中
    # 当前值大于队列最后一个元素时，将此时队列最后一个元素弹出，因此q[0]记录的一定是最大值对应的下标
    for i in range(k):
        while q and nums[i] >= nums[q[-1]]:
            q.pop() 
        q.append(i)
    max_num = [q[0]]
    # 这里所做的操作和上述原理一样
    # 不同的是加入左边界的判断
    for i in range(k,len(nums)):
        while q and nums[i] >= nums[q[-1]]:
            q.pop() 
        q.append(i)
        while q[0] <= i-k:
            q.popleft()
        max_num.append(nums[q[0]])
    return max_num

总结：

这里新提出来两个数据结构：优先队列和单调队列

优先队列这里用了heap来实现，总的来说，这个解法是：

在第一次建堆之后，位于堆顶的元素就是目前的最大值「优先级最高」了，之后随着滑动窗口向右滑动，我们往这个堆中添加当前元素并调整堆。此时我们左边的元素还没有弹出，因此我们需要判断当前最大值是不是没有在滑动窗口内，否则的话就需要把左边的元素弹出堆（保证最大值在当前滑动窗口内）
优先队列是一种数据结构，其中每个元素都有一个优先级，元素按优先级进行排序和访问。通常，优先队列支持以下操作：
1. 插入元素：将一个元素加入队列中。
2. 取出优先级最高的元素：移除/返回优先级最高的元素。
优先队列可以使用多种数据结构来实现，例如堆（Heap），其中二叉堆是最常用的一种实现方式。
单调队列这里用了deque来实现，总的来说，这个解法是：

先来个前提，q是一个单调队列，他会将左边比他小的都弹出去，也因此它是一个单调递减的队列，nums[q[0]]就是当前最大值。

我们也需要来判断q[0]的位置是否在滑动窗口内。

这样的好处是我们不需要频繁的调整堆来获取最大值，只需要维护这个队列。

单调队列是一种特殊类型的队列，具有单调性的约束，即队列中的元素按某种单调性排列。单调队列可以是单调递增队列或单调递减队列

单调队列通常用于滑动窗口问题，其中需要在固定窗口内快速获取最大值或最小值。
在Python的collections.deque中，pop和popleft方法都用于移除元素，但它们的操作位置不同：
- **pop()**：从双端队列的右端（末尾）移除并返回一个元素。
- **popleft()**：从双端队列的左端（开头）移除并返回一个元素。

12. 76: 最小覆盖子串

#哈希表 #字符串 #滑动窗口

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

解决：

滑动窗口+哈希表

from calendar import c
from collections import Counter
from tkinter import N

def minWindow(s, t):
    # 判断s和t是否为空，或者s的长度是否小于t的长度
    if not s or not t or len(s) < len(t):
        return ''
    # 答案
    ans = float('inf'), None, None
    
    # 左右指针
    left = 0
    right = 0
    
    # t中每个字符出现的次数
    counter_t = Counter(t)
    # s中每个字符出现的次数
    counter_s = Counter()
    
    # 记录当前窗口中符合条件的字符个数
    required = 0
    
    while right < len(s):
        character = s[right]
        counter_s[character] += 1
        # 判断当前字符是否在t中且在当前窗口中出现的次数已满足（>=）在t中出现的次数
        if character in counter_t and counter_s[character] == counter_t[character]:
            required += 1
        # 当前窗口中的字符已经满足t中的所有字符
        while left <= right and required == len(counter_t):
            character = s[left]
            # 更新最小窗口  
            if right - left + 1 < ans[0]:
                ans = (right - left + 1, left, right)
            
            # 左指针右移前将当前字符在窗口中出现的次数减1
            counter_s[character] -= 1
            # 判断当前字符是否在t中且在当前窗口中出现的次数已不满足（<）在t中出现的次数
            if character in counter_t and counter_s[character] < counter_t[character]:
                required -= 1
            
            # 左指针右移
            left += 1
        right += 1
    return "" if ans[0] == float("inf") else s[ans[1]: ans[2] + 1]

总结：

有两个思路被广泛使用：
1. 第一个是遇到字母异位词 / 子串被包含等关系时候可以用Hash表来计数。
2. 滑动窗口的使用，一般right指针随着循环便利，我们需要关注的是left指针移动的条件。
还有Counter的使用，用来统计出现的次数

普通数组

13. 53: 最大子数组和

#数组 #最大前缀和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

解决：

def maxSubArray(nums):
    maxSum = [0] * (len(nums))
    maxSum[0] = nums[0]
    for i in range(1, len(nums)):
        maxSum[i] = nums[i] + max(maxSum[i-1],0)
        
    return max(maxSum)

总结：

和求解“和为 K 的子数组”这道题类似，用到了前缀和这个思想，但是这儿是最大前缀和，很巧妙。

14. 56: 合并区间

#数组 #排序

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi]。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

解决：

def merge(intervals: list[list[int]]) -> list[list[int]]:
    intervals.sort(key = lambda x:x[0])
    merged = []
    for interval in intervals:
        if not merged or merged[-1][1] < interval[0]:
            merged.append(interval)
        else:
            merged[-1][1] = max(merged[-1][1], interval[1])
    return merged

15. 189: 轮转数组

#数组 #数学 #双指针

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

解决：

def rotate(nums, k):
    """
    :type nums: List[int]
    :type k: int
    :rtype: None Do not return anything, modify nums in-place instead.
    """
    ex_num = k % len(nums)
    new_nums = [0] * len(nums)
    for i in range(len(nums)):
        new_pos = (i + ex_num) % len(nums)
        new_nums[new_pos] = nums[i]
    nums[:] = new_nums

总结：

nums[:] = new_nums 和 nums = new_nums

Algorithm > LeetCode

#LeetCode

LeetCode

https://adzuki23.github.io/2024/06/28/LeetCode/

作者

Hongyu Li

发布于

2024年6月28日

更新于

2024年7月30日

许可协议

AIGC-StableDiffusion 上一篇

Interview Direction Series 下一篇