LLM-Transformer

[TOC]

Transformer

Transformer 模型是由谷歌在2017 年提出并首先应用于机器翻译的神经网络模型结构。Transformer 结构完全通过注意力机制完成对源语言序列和目标语言序列全局依赖的建模。

参考文章：

本文只是做一些学习记录总结，内容全部来源于作者猛猿以下文章，写的非常详细：

https://zhuanlan.zhihu.com/p/454482273、https://zhuanlan.zhihu.com/p/456863215等

结构图：

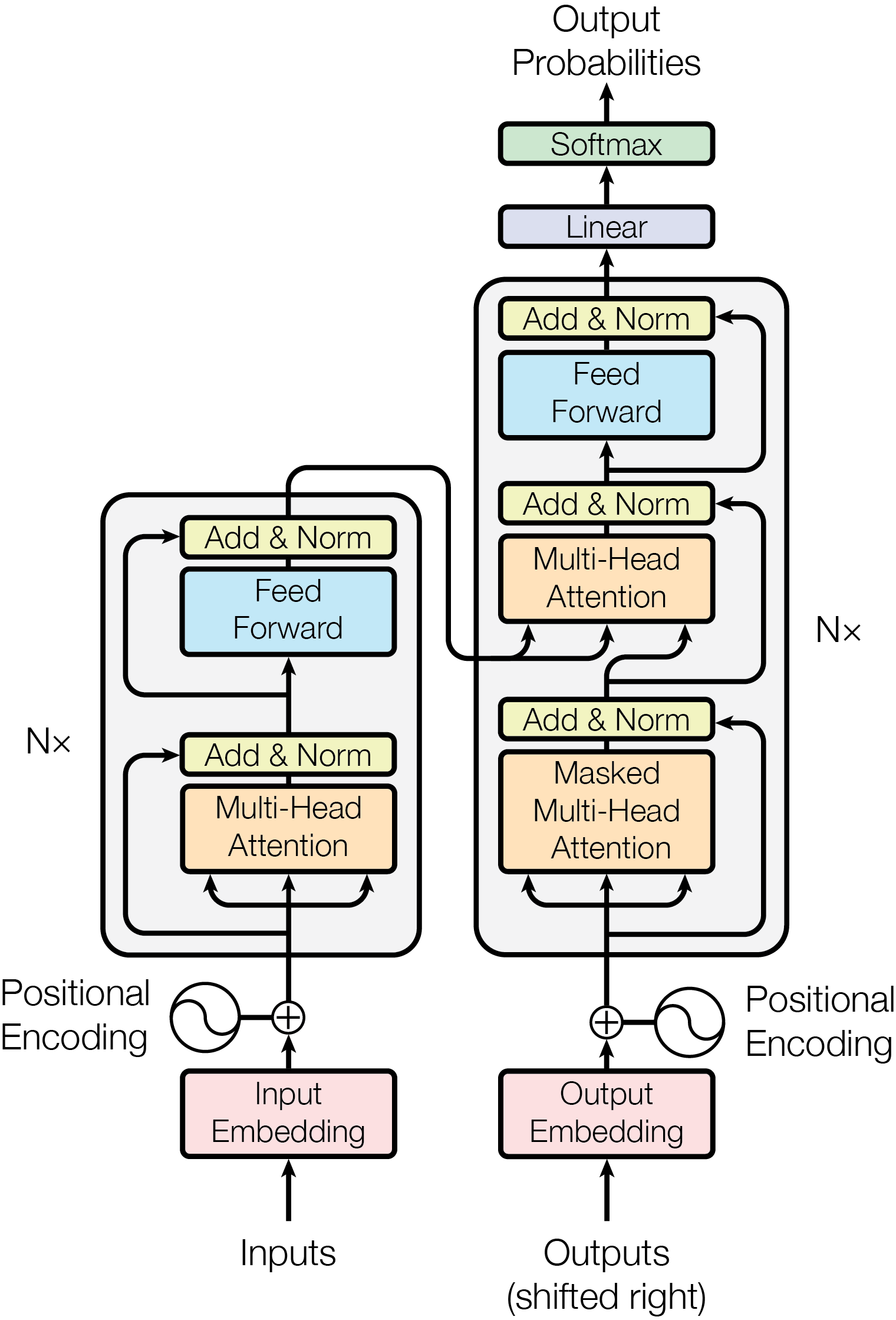
1. 位置编码

---

在Transformer的encoder和decoder的输入层中，使用了Positional Encoding，使得最终的输入满足：

$input = Input\ Embedding + Positional\ Encoding$

1.1 为什么需要位置编码：

在self-attention模型中，输入是一整排的tokens，对于人来说，我们很容易观察到tokens的位置信息，但是因为self-attention的运算是无向的，无法分辩tokens位置信息，因此我们要想办法，把tokens的位置信息，喂给模型。

1.2 如何构造位置编码

一些方法，比如 用整型值标记位置 / 用[0,1]范围标记位置 / 用二进制向量标记 / 用周期函数sin表示….等，都有其不足之处和局限性。

但我们有一些希望实现的目标：

• 位置的表示应该是有界的；
• 模型可以处理在训练时没见过的句子长度；
• 序列长度不同时，tokens的相对位置应该保持一致；
• 希望位置编码在连续空间内而不是离散的；
• 不同的位置向量是可以通过线性转换得到的。

1.2.1用周期函数 Sin 表示Position Encoding:

我们把位置向量当中的每一个元素都用一个sin函数来表示，则第t个token的位置向量可以表示为：
$$
PE_t = [\sin(\frac{1}{2^0}t), \sin(\frac{1}{2^1}t),\cdots,\sin(\frac{1}{2^{i-1}}t),\cdots,\sin(\frac{1}{2^{d_{model}-1}}t)]
$$
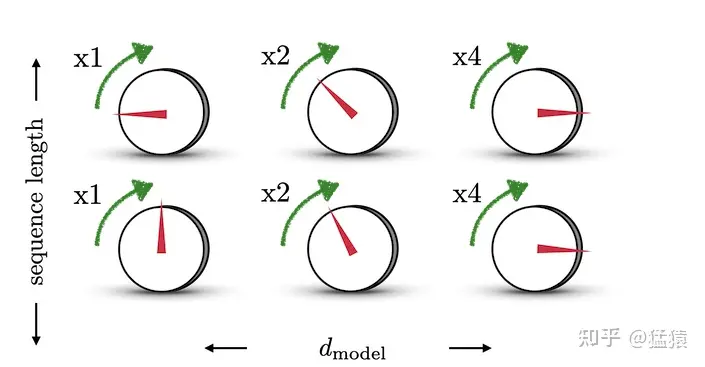
结合下图，来理解一下这样设计的含义，图中每一行表示一个$PE_t$ ，每一列表示$PE_t$ 中的第i个元素。d_model表示token的维度。

旋钮用于调整精度，越往右边的旋钮，需要调整的精度越大，因此指针移动的步伐越小。每一排的旋钮都在上一排的基础上进行调整（函数中 t 的作用）。通过频率$\frac{1}{2^{i-1}}$来控制sin函数的波长，频率不断减小，则波长不断变大，此时sin函数对t的变动越不敏感，以此来达到越向右的旋钮，指针移动步伐越小的目的。 这也类似于二进制编码，每一位上都是0和1的交互，越往低位走（越往左边走），交互的频率越慢。

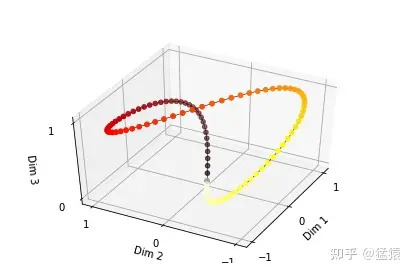
由于sin是周期函数，因此从纵向来看，如果函数的频率偏大，引起波长偏短，则不同t下的位置向量可能出现重合的情况。比如在下图中(d_model = 3），图中的点表示每个token的位置向量，颜色越深，token的位置越往后，在频率偏大的情况下，位置响亮点连成了一个闭环，靠前位置（黄色）和靠后位置（棕黑色）竟然靠得非常近：

为了避免这种情况，我们尽量将函数的波长拉长。一种简单的解决办法是同一把所有的频率都设成一个非常小的值。因此在transformer的论文中，采用了$\frac{1}{10000^{i/{d_{model}-1}}}$这个频率（这里 i 其实不是表示第 i 个位置，但是大致意思差不多，下面会细说）

总结一下，到这里我们把位置向量表示为：其中$w_i$等于$\frac{1}{10000^{i/{d_{model}-1}}}$
$$
PE_t = [\sin(w_0t), \sin(w_1t),\cdots,\sin(w_{i-1}t),\cdots,\sin(w_{d_{model}-1}t)]
$$

1.2.2 用sin和cos交替来表示位置

目前为止，我们的位置向量实现了如下功能：

• 每个token的向量唯一（每个sin函数的频率足够小）；
• 位置向量的值是有界的，且位于连续空间中。模型在处理位置向量时更容易泛化，即更好处理长度和训练数据分布不一致的序列（sin函数本身的性质）。

那现在我们对位置向量再提出一个要求：不同的位置向量是可以通过线性转换得到的。这样，我们不仅能表示一个token的绝对位置，还可以表示一个token的相对位置，即我们想要：
$$
PE_{t+\triangle{t}}=T_{\triangle{t}}*PE_t
$$
这里，$T$ 表示一个线性变换矩阵。观察这个目标式子，联想到在向量空间中一种常用的线形变换—旋转。在这里，我们将t想象为一个角度，那么$\triangle{t}$就是其旋转的角度，则上面的式子可以进一步写成：

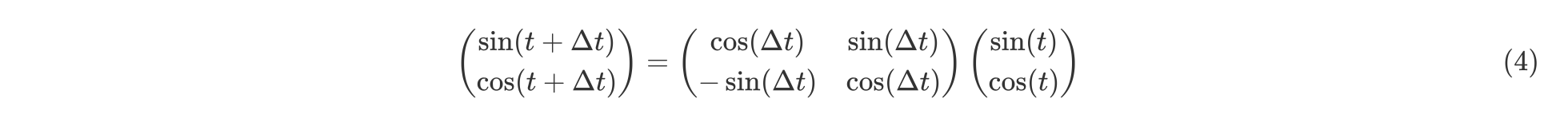
有了这个构想，我们就可以把原来元素全都是sin函数的 做一个替换，我们让位置两两一组，分别用sin和cos的函数对来表示它们，则现在我们有：
$$
PE_t = \sin(w_0t),\cos(w_0t),\sin(w_1t),\cos(w_1t)\cdots,\sin(w_{i-1}t),\cos(w_{i-1}t),\cdots,\sin(w_{d_{model}-1}t),\cos(w_{d_{model}-1}t)
$$
在这样的表示下，我们可以很容易用一个线性变换，把$PE_t$转变为$PE_{t+\Delta t}$ ，具体公式参考文章。

1.3 Transformer中位置编码方法：Sinusoidal functions

定义：

• t 是这个token在序列中的实际位置（例如第一个token为1，第二个token为2…）
• $PE_t\in\mathbb{R^d}$是这个token的位置向量， $PE_t^{(i)}$表示这个位置向量里的第i个元素
• $d_{model}$是这个token的维度（在论文中，是512)

$PE_t^{(i)}$则可以如下表示，这里$w_k=\frac{1}{10000^{2k/{d_{model}-1}}}$，$k=0,1,2,3,\dots,\frac{d_{model}}{2}-1$
$$
PE_t^{(i)} = \begin{cases}
\sin(w_kt) & \text{if } i = 2k \
\cos(w_kt) & \text{if } i = 2k+1
\end{cases}
$$
这个意思和式子(5)中的意思是一模一样的，把512维的向量两两一组，每组都是一个sin和一个cos，这两个函数共享同一个频率$w_i$ ，一共有256组，由于我们从0开始编号，所以最后一组编号是255。sin/cos函数的波长（由$w_i$决定）则从$2\pi$增长到 $2\pi*10000$

1.4 Transformer位置编码可视化

下图是一串序列长度为50，位置编码维度为128的位置编码可视化结果：

可以发现，由于sin/cos函数的性质，位置向量的每一个值都位于[-1, 1]之间。同时，纵向来看，图的右半边几乎都是蓝色的，这是因为越往后的位置，频率越小，波长越长，所以不同的t对最终的结果影响不大。而越往左边走，颜色交替的频率越频繁。

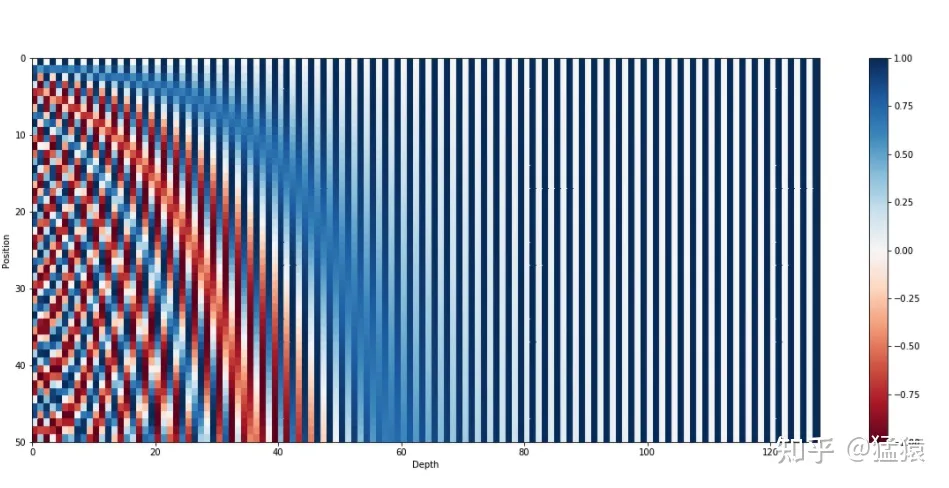
1.5 Transformer位置编码的重要性质

1. 两个位置编码的点积(dot product)仅取决于偏移量$\Delta t$ ，即两个位置编码的点积可以反应出两个位置编码间的距离。

   

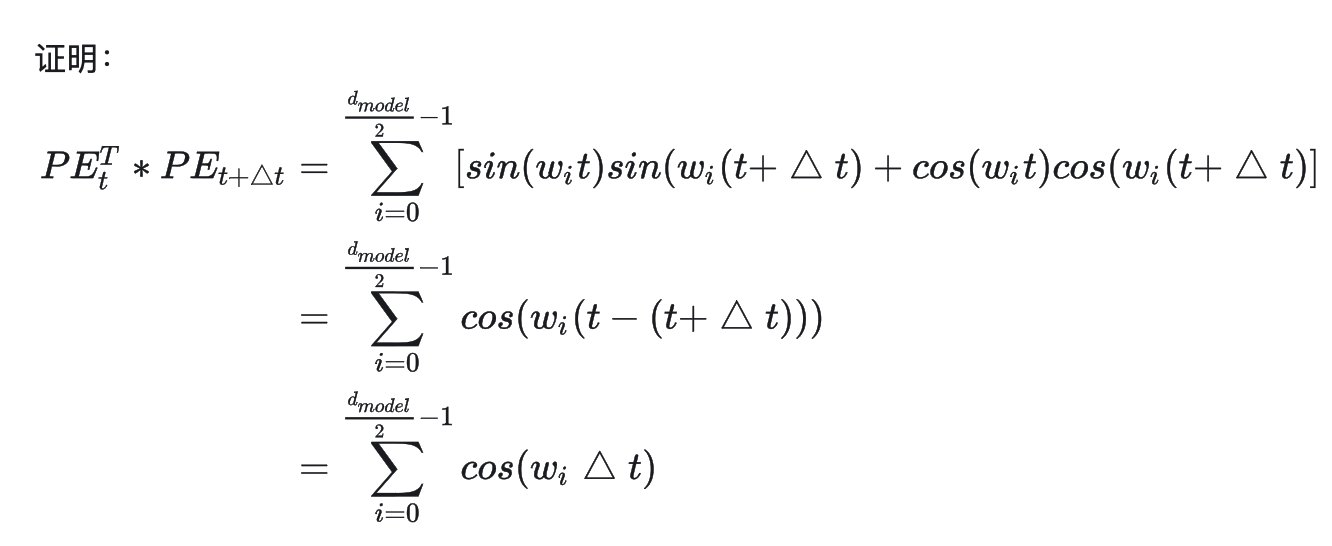
2. 位置向量的点积可以用于表示距离(distance-aware)，但是它却不能用来表示位置的方向性(lack-of-directionality)。

3. 在Transformer的论文中，比较了用positional encoding和learnable position embedding(让模型自己学位置参数）两种方法，得到的结论是两种方法对模型最终的衡量指标差别不大。不过在后面的BERT中，已经改成用learnable position embedding的方法了，也许是因为positional encoding在进attention层后一些优异性质消失的原因（猜想）。Positional encoding有一些想象+实验+论证的意味，而编码的方式也不只这一种，比如把sin和cos换个位置，依然可以用来编码。

2.Self-Attention（自注意力机制）

---

2.1 Attention构造

在RNN当中，tokens是一个一个被喂给模型的。比如在x3的位置，模型要等x1和x2的信息都处理完成后，才可以处理x3。

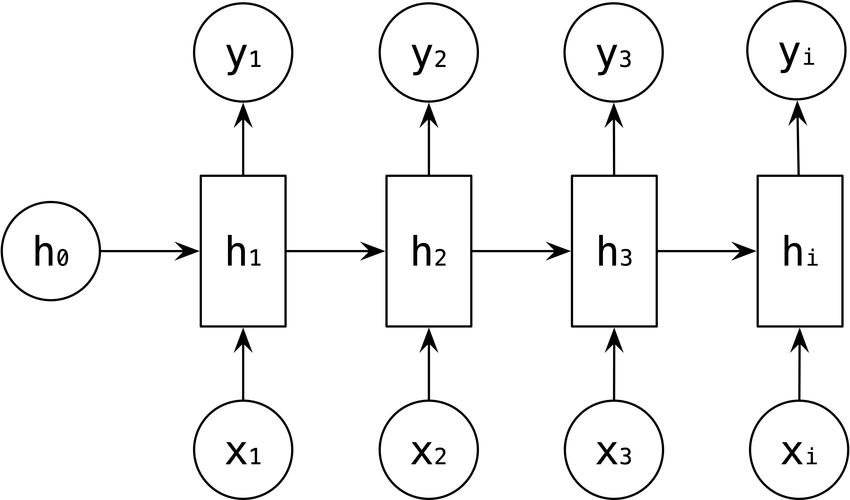
这种构造造成的缺点：

1. Sequential operations的复杂度随着序列长度的增加而增加。
   这是指模型下一步计算的等待时间，在RNN中为O(N)。该复杂度越大，模型并行计算的能力越差，反之则反。

2. Maximum Path length的复杂度随着序列长度的增加而增加。
   这是指信息从一个数据点传送到另一个数据点所需要的距离，在RNN中同样为O(N)，距离越大，则在传送的过程中越容易出现信息缺失的情况，即数据点对于远距离处的信息，是很难“看见”的。

那么，在处理序列化数据的时候，是否有办法，在提升模型的并行运算能力的同时，对于序列中的每个token，也能让它不损失信息地看见序列里的其他tokens呢？ Attention就作为一种很好的改进办法出现了。每个token生成其对应的输出的过程是同时进行的，计算不需要等待。

2.2 Attention计算过程图解

query，key，value的产生：

假设batch_size=1，输入序列X的形状为(seq_len = 4, d_model = 6)，则对于这串序列，我们产生三个参数矩阵：$W^Q、W^K、W^V$ 。通过上述的矩阵乘法，我们可以得到最终的结果Q，K，V。如下图所示：

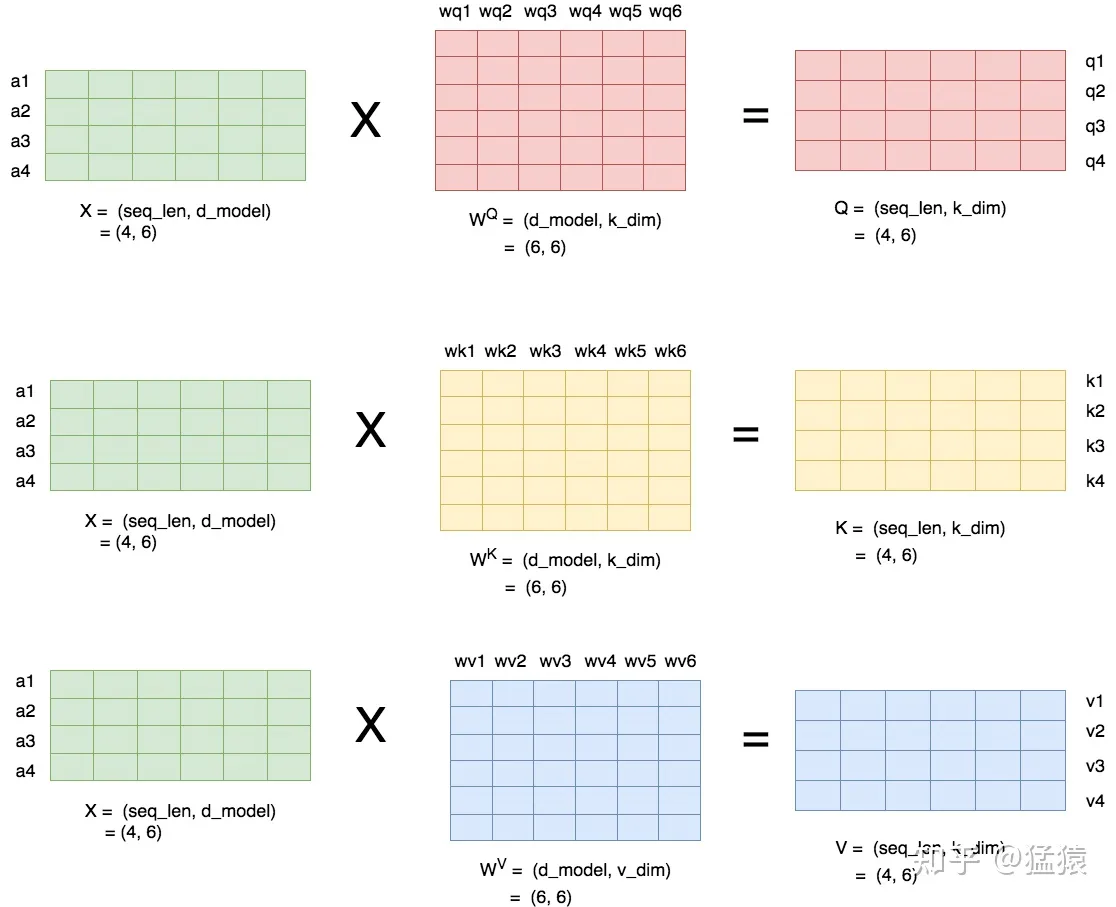
一般来说， $W^Q$和$W^K$都同样使用$k_{dim}$， $W^V$使用$v_{dim}$。

$k_{dim}$和$v_{dim}$不一定要相等，但在transformer的原始论文中，采用的策略是：$K_{dim}=V_{dim}=d_{model}//n_{heads}$，其中$n_{heads}$为self-attention的头数。

query，key，value的意义：

• query向量类比于询问。某个token问：“其余的token都和我有多大程度的相关呀？”

  Query用于与Key矩阵进行点积操作，以计算当前输入与所有输入之间的相似度或关联程度。这个相似度决定了当前输入关注其他输入的程度。

• key向量类比于索引。某个token说：“我把每个询问内容的回答都压缩了下装在我的key里”

  Key矩阵代表所有输入中每个单词（或输入）的特征，用于匹配Query以计算相似度。通过点积操作，Key帮助Query找到相关性高的输入。

• value向量类比于回答。某个token说：“我把我自身涵盖的信息又抽取了一层装在我的value里”

  Value矩阵代表所有输入中每个单词（或输入）的实际信息值，它是最终的加权结果。Value提供实际的信息内容，它会根据计算得到的注意力分数进行加权平均，从而得到每个输入的最终表示。这些加权后的值将被用于后续的层或输出。

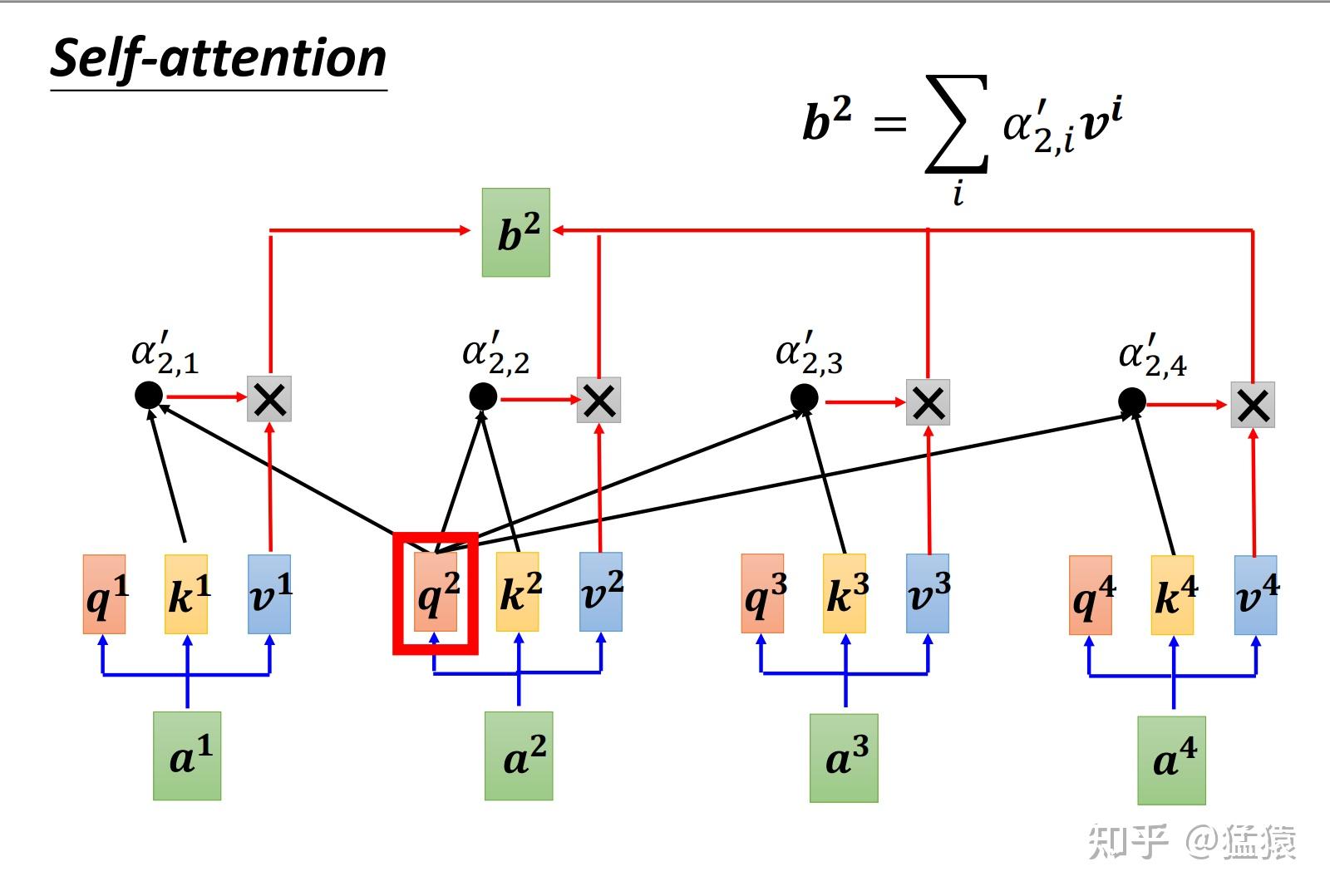
以图中的token a2为例：

• 它产生一个query，每个query都去和别的token的key做“某种方式”的计算，得到的结果我们称为attention score（即为图中的$\alpha_{2,i}’$）。则一共得到四个attention score（attention score又可以被称为attention weight）。
• 将这四个score再分别乘上每个token的value，我们会得到四个抽取信息完毕的向量。
• 将这四个向量相加，就是最终a2过attention模型后所产生的结果b2。

2.3 Attention Score 计算

$$
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V
$$

其中$d_k$就是$k_{dim}$，而$softmax(\frac{QK^T}{\sqrt{d_k}})$就是Attention Score矩阵，我们来详细看下这个矩阵的计算过程:

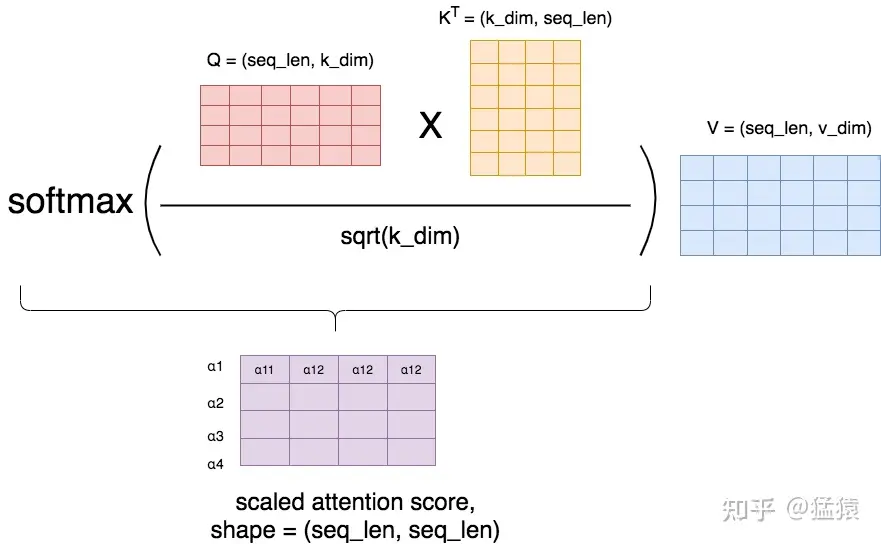
（勘误：紫色方框中的下标有误 )

在softmax之后，attention score矩阵的每一行表示一个token，每一列表示该token和对应位置token的$\alpha$值，因为进行了softmax，每一行的$\alpha$值相加等于1。

论文中所采用的是scaled dot-product，因为乘上了因子$1/\sqrt{d_k}$​ ，乘因子$1/\sqrt{d_k}$ 的原因是为了使得在softmax的过程中，梯度下降得更加稳定，避免因为梯度过小而造成模型参数更新的停滞。下面我们通过数学证明，来解释这个结论：

---

假设输入向量 ( q ) 和 ( k ) 的各个分量是独立同分布的随机变量，均值为0，方差为1，则q、k的点积的期望值和方差为：

期望：$\mathbb{E}[q \cdot k] = 0$；方差：$\text{Var}(q \cdot k) = d_k$

如果不进行缩放，点积的方差为 ( $d_k$ )，随着 ( $d_k$ ) 增大，点积的值会变得越来越大，这会导致Softmax函数的输入值也变大，从而使得Softmax函数的梯度变得很小，如下所示。通过乘以 ($ \frac{1}{\sqrt{d_k}}$ )，点积的方差变为1，这样可以使得点积的值在一个较小的范围内波动，保持数值稳定性，避免梯度消失问题。加上下图进行理解：

---

2.4 Masked Attention

在transformer的decoder层中，我们用到了masked attention。在序列生成任务（如机器翻译或文本生成）中，模型在生成第t个位置的单词时，不应该看到第t+1个位置及其之后的单词。Masked Attention通过掩码来阻止模型在计算当前位置的注意力权重时访问未来的位置，从而避免了信息泄露。

具体来说，在实现Masked Attention时，通常会构建一个上三角形矩阵掩码，这个掩码矩阵的下三角部分为1（允许注意），上三角部分为0（屏蔽注意）。在计算注意力权重时，这个掩码矩阵会被加到注意力分数上，通过对屏蔽位置施加一个大的负数，从而在softmax计算时将这些位置的权重归零。示例代码如下：

import torch
import torch.nn.functional as F

def masked_attention(Q, K, V, mask):
    scores = torch.matmul(Q, K.transpose(-2, -1)) / (K.size(-1) ** 0.5)
    scores = scores.masked_fill(mask == 0, float('-inf'))
    attention_weights = F.softmax(scores, dim=-1)
    output = torch.matmul(attention_weights, V)
    return output

# 示例输入
Q = torch.rand(2, 3, 4)  # (batch_size, seq_length, d_k)
K = torch.rand(2, 3, 4)
V = torch.rand(2, 3, 4)
mask = torch.tril(torch.ones(3, 3)).unsqueeze(0).repeat(2, 1, 1)  # 下三角掩码

output = masked_attention(Q, K, V, mask)

2.5 Multihead Attention

多头注意力通过多个并行的注意力头来处理输入，每个注意力头可以关注输入序列的不同部分或不同的特征子空间。这样，模型能够捕获更丰富、更细粒度的信息，而不是单一头注意力所能提供的有限视角。

不同的注意力头可以学习到不同类型的关系和模式，这使得模型在处理复杂的序列关系时更具灵活性和表达力。例如，一个注意力头可能专注于短距离依赖关系，而另一个注意力头可能专注于长距离依赖关系。

在NLP中，这种模式识别同样重要。比如第一个head用来识别词语间的指代关系(某个句子里有一个单词it，这个it具体指什么呢），第二个head用于识别词语间的时态关系（看见yesterday就要用过去式）等等。

具体实现上，多头注意力通过以下步骤实现：

1. 线性变换：输入的查询（Q）、键（K）、值（V）向量分别经过线性变换，得到多个头的Q‘、K’、V‘。

2. 独立计算注意力：对每个头的Q、K、V分别计算注意力权重，并对V进行加权求和。

3. 连接和线性变换：将所有头的输出连接在一起，并通过一个线性变换得到最终的输出。

示例代码如下：

import torch
import torch.nn as nn

class MultiheadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super(MultiheadAttention, self).__init__()
        assert d_model % num_heads == 0
        self.d_k = d_model // num_heads
        self.num_heads = num_heads

        self.linear_Q = nn.Linear(d_model, d_model)
        self.linear_K = nn.Linear(d_model, d_model)
        self.linear_V = nn.Linear(d_model, d_model)
        self.linear_out = nn.Linear(d_model, d_model)

        self.attention = nn.MultiheadAttention(embed_dim=d_model, num_heads=num_heads)

    def forward(self, Q, K, V, mask=None):
        batch_size = Q.size(0)

        # 线性变换并分割成多头
        '''
        view操作将Q的形状从 (batch_size, seq_length, d_model) 转换为 (batch_size, seq_length, num_heads, d_k)，
        其中 d_k = d_model // num_heads。具体来说，这一步通过view将d_model维度拆分成两个维度：num_heads和d_k。
        transpose操作交换了第1维和第2维，使得Q的形状变为 (batch_size, num_heads, seq_length, d_k)。
        这是因为我们希望将多个头分开处理，而不是在序列长度维度上处理。
        '''
        Q = self.linear_Q(Q).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        K = self.linear_K(K).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        V = self.linear_V(V).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

        # 计算注意力
        scores = torch.matmul(Q, K.transpose(-2, -1)) / (self.d_k ** 0.5)
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))
        attention_weights = torch.nn.functional.softmax(scores, dim=-1)
        attention_output = torch.matmul(attention_weights, V)

        # 连接多头输出并进行线性变换
        attention_output = attention_output.transpose(1, 2).contiguous().view(batch_size, -1, self.num_heads * self.d_k)
        output = self.linear_out(attention_output)

        return output

# 示例输入
d_model = 512
num_heads = 8
# (batch_size, seq_length, d_model)
Q = torch.rand(2, 10, d_model) 
K = torch.rand(2, 10, d_model)
V = torch.rand(2, 10, d_model)
mask = None

multihead_attention = MultiheadAttention(d_model, num_heads)
output = multihead_attention(Q, K, V, mask)

3.Layer Normalization（层归一化）

3.1 Batch Normalization

Batch Normalization（以下简称BN）的方法最早由Ioffe&Szegedy在2015年提出，主要用于解决在深度学习中产生的内部协变量偏移-ICS（Internal Covariate Shift）的问题。在BasicKnowledge那篇文章中我们详细介绍了Batch Normalization的原理和作用。Batch Normalization被广泛用在CNN任务上来处理图像，针对文本任务，它有以下缺点：

1. “长短不一”：文本中某些位置没有足够的batch的数据，使得计算出来的$\mu$ 、$\sigma ^2$产生偏差。
2. 测试集中出现比训练集更长的数据，由于BN在训练中累积 ，在测试中使用累计的经验统计量的原因，导致测试集中多出来的数据没有相应的统计量以供使用。 （在实际应用中，通常会对语言类的数据设置一个max_len，多裁少pad，这时没有上面所说的这个问题。但这里我们讨论的是理论上的情况，即理论上，诸如Transformer这样的模型，是支持任意长度的输入数据的）。
3. 在 RNN 中，每个时间步的数据依赖于前面时间步的隐藏状态。Batch Normalization 对当前时间步的数据进行归一化时引入了整个批次的信息，可能会破坏这种依赖关系。例如，某个时间步的输入特征会因批次内其他时间步的均值和方差的变化而变化，从而影响隐藏状态的更新。这破坏了 RNN 模型逐步构建时间依赖性的能力。

3.2 Layer Normalization

做法：

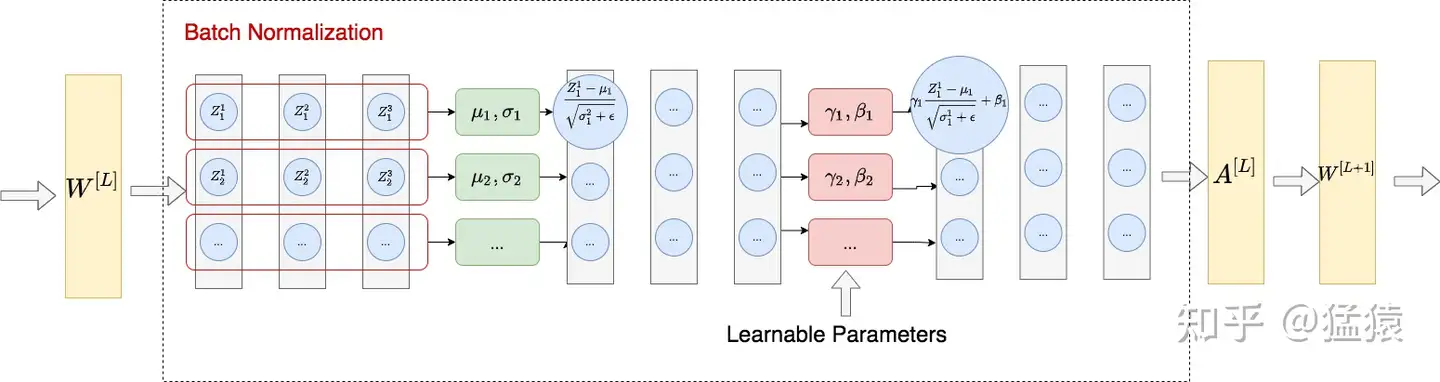
Layer Normalization整体做法类似于BN，不同的是LN不是在特征维度间进行标准化操作（横向操作），而是在整条数据间进行标准化操作（纵向操作）。以图像任务为例：

BN：对一个batch里同一channel上的所有数据求取均值和方差

LN：在一张图片里所有channel的pixel范围内计算均值和方差

以下图为例：$Z^i_j$：i表示第几个样本，j表示维度

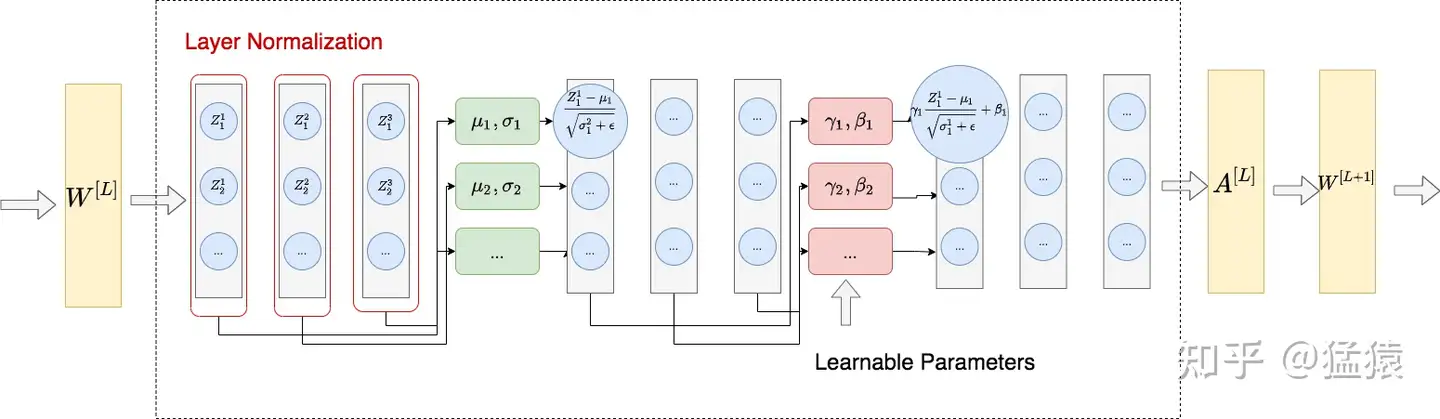
优点：

LN使得各条数据间在进行标准化的时候相互独立，因此LN在训练和测试过程中是一致的。LN不需要保留训练过程中的 ，每当来一条数据时，对这条数据的指定范围内单独计算所需统计量即可。

3.3 Transformer LN改进方法：Pre-LN

原始transformer中，采用的是Post-LN，即LN在residule block（图中addtion）之后。Xiong et al. (2020)中提出了一种更优Pre-LN的架构，即LN在residule block之前，它能和Post-LN达到相同甚至更好的训练结果，同时规避了在训练Post-LN中产生的种种问题。两种架构的具体形式可以见下图。

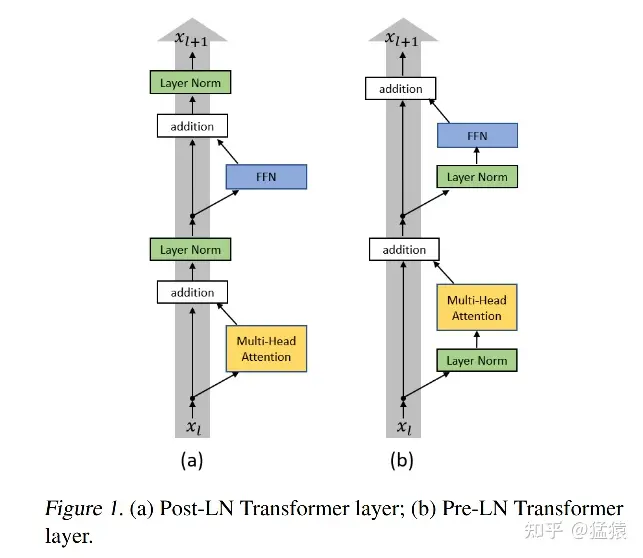
Post-LN 是原始 Transformer 论文中的默认设置。在这种情况下，学习率 warm-up 策略显得尤为重要，因为 Post-LN 的训练可能会不稳定，尤其是深层模型中。Warm-up 可以帮助缓解这种不稳定性，具体原因如下：

Warm-up：是一种在训练初期使用较低学习率的策略，然后逐步增加到目标学习率的技术。其目的是稳定训练过程，并防止梯度消失或爆炸问题。

训练初期稳定性：在模型训练初期，参数初始化较为随机，直接使用较大的学习率可能导致梯度过大，参数更新幅度过大。Warm-up 可以平缓地增加学习率，使模型逐步适应训练数据，减少训练初期的震荡。

梯度问题：Post-LN 中，归一化层在残差连接之后，可能导致梯度传播过程中逐层缩小。Warm-up 阶段的低学习率可以在一定程度上防止梯度消失或爆炸问题。

Pre-LN为什么比Post-LN更好：

在Post-LN结构中，Layer Normalization在残差连接之后进行。这意味着经过一个子层的输出在与输入相加之后，再经过归一化处理。这种设置的潜在问题是：虽然残差连接有助于梯度的流动，但归一化操作可能会在反向传播中影响梯度的大小，尤其是在深层网络中，这可能导致梯度逐层减小。这种现象类似于梯度消失的表现，但它不是因为归一化本身，而是因为归一化操作的位置和对梯度的调节作用。

Pre-LN的一个主要优势是，它在Layer Normalization之后再进行残差连接，这样可以使得Layer Normalization不会直接作用于反向传播中的梯度。这种设置可以使梯度在反向传播时更加稳定，减小梯度逐层缩小的问题。

4. ResNet（残差网络）

弄清楚一个问题：为什么「嵌入/每一层输出」需要再次输入到 Add & Norm 层？

梯度传递的稳定性：残差连接使得梯度可以直接通过加法路径传递，从而缓解深层网络中的梯度消失问题。

模型收敛性和训练速度：归一化操作确保了每一层的输入分布是稳定的，有助于模型的快速收敛。

信息保留：通过残差连接，输入信息不会在每一层中丢失，而是持续传递到更深层次的网络中。

下列代码示例中输入嵌入 x 直接加到多头注意力层的输出 sublayer_output 上，然后进行层归一化，输出的形状与输入相同。通过这种设计，确保了每一层的输出在传递过程中保持稳定并保留原始信息。

import torch
import torch.nn as nn

class AddNorm(nn.Module):
    def __init__(self, d_model, dropout=0.1):
        super(AddNorm, self).__init__()
        self.norm = nn.LayerNorm(d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer_output):
        return self.norm(x + self.dropout(sublayer_output))

# 示例输入
batch_size = 2
seq_length = 10
d_model = 512

x = torch.rand(batch_size, seq_length, d_model)  # 输入嵌入
sublayer_output = torch.rand(batch_size, seq_length, d_model)  # 多头注意力层的输出

# Add & Norm 层
add_norm = AddNorm(d_model)
output = add_norm(x, sublayer_output)

print(output.shape)  # (batch_size, seq_length, d_model)

6. 其他

6.1 weight tying

在Transformer模型中，weight tying 是一种减少模型参数数量的方法。具体而言，它是在多个不同的层之间共享权重。这种技术可以显著降低模型的参数数量，从而减小模型的复杂性和内存占用，同时还能帮助模型在训练时更好地泛化。

在Transformer模型中，最常见的weight tying场景有两个：

1. Embedding层和输出层之间的weight tying：

   在自然语言处理（NLP）任务中，输入的词嵌入（word embeddings）和输出的词概率分布（通常通过softmax层得到）都需要一个词汇表大小的矩阵。通常情况下，这两个矩阵是独立的，但通过weight tying，这两个矩阵可以共享同一个权重。

   这种共享可以通过以下方式实现：假设输入的词嵌入矩阵为 E ，输出层的权重矩阵为 W ，则通过将 W 设置为 $E^T $ 来实现共享。

   import torch
   import torch.nn as nn
   
   class TransformerModel(nn.Module):
       def __init__(self, vocab_size, d_model):
           super(TransformerModel, self).__init__()
           self.embedding = nn.Embedding(vocab_size, d_model)
           self.transformer = nn.Transformer(d_model)
           self.fc_out = nn.Linear(d_model, vocab_size)
   
           # Weight tying: set the output layer weights to be the same as the embedding layer weights
           self.fc_out.weight = self.embedding.weight
   
       def forward(self, src, tgt):
           src_emb = self.embedding(src)
           tgt_emb = self.embedding(tgt)
           transformer_output = self.transformer(src_emb, tgt_emb)
           output = self.fc_out(transformer_output)
           return output
   
   # 示例参数
   vocab_size = 10000  # 词汇表大小
   d_model = 512       # 嵌入维度
   
   # 创建模型实例
   model = TransformerModel(vocab_size, d_model)

2. Encoder和Decoder之间的weight tying：

   在一些Seq2Seq模型（如翻译模型）中，编码器和解码器可以使用相同的权重。这种共享可以通过将编码器和解码器的相应层设置为相同的权重来实现。