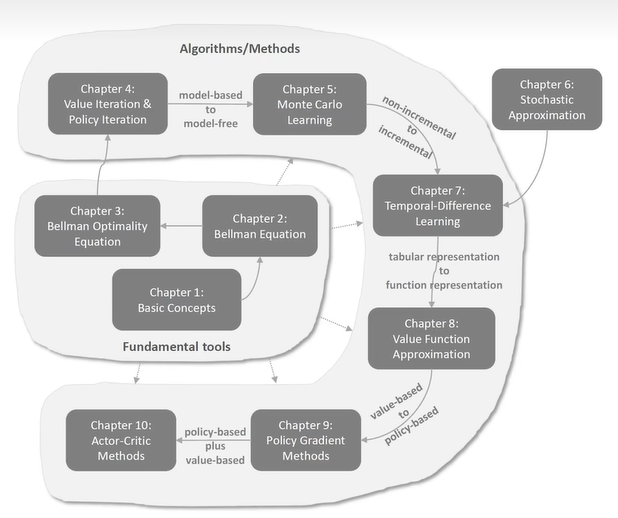
Reinforcement Learning

[TOC]

Reinforcement Learning

强化学习的目标：找到最优策略

基本概念

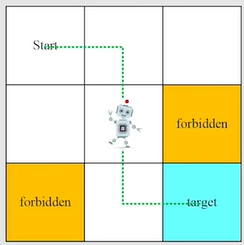
以grid-world [网格世界] 为例：

1. State

agent相对于environment的状态，在grid-world中是指agent的location。

在FrozenLake这个小游戏中就是以0-15表示所处位置来表示State，

更复杂的情况可以其它state，比如agent的速度、加速度等等。把所有状态放到一起就得到了State space。表示为$S={s_i} $

2. Action

对于每一个状态，有一系列可采取的行动。在grid-world中是指up、down、left、right、stay这五个动作。把所有动作放到一起就得到了Action space。特别的是，不同状态下的Action Space是不一样的，因此表示为$A(s_i)={a_i} $

3. State transition

当采取一个Action时，agent从一个状态s1移动到另一个状态s2。

3.1 Tabular

我们可以用表格的方式来罗列出所有可能性，但是有个局限，它只能表示确定的情况，如果agent向上走可能被弹到s1，s4，甚至被连续弹到s7这些情况，就无法用表格的方法。

3.2 State transition probability

引入条件概率来描述state transition，下列公式还是用的确定性例子。
$$
p(s_2|s_1,a2)=1 \
p(s_i|s_1,a2)=0
$$

4. Policy

告诉agent，如果我在状态$S_i$，我应该采取什么action。

用数学的表达方式–条件概率来描述它，在强化学习中 $\pi$ 表示为策略，下面的式子表示在$s_1$的状况下，采取各个action的概率：
$$
\pi(a_1|s_1)=0\
\pi(a_2|s_1)=0.5\
\pi(a_3|s_1)=0.5\
\pi(a_4|s_1)=0\
\pi(a_5|s_1)=0
$$

5. Reward

采取了action后得到的一个实数，正数表示鼓励，负数表示惩罚。

5.1 Tabular

对于一些确定的状况（执行一个action一定会得到确定的reward），可以用表格表示法。

例子见补充-【Q表–FrozenLake游戏】

5.2 Conditional probability

对于一些不确定的情况，可以用数学的表达方式–条件概率来表示。

比如当前在$s_1$，如果我们选择了$a_1$，得到reward为-1的概率为：$p(r=1|s_1,a_1)$

6. Trajectory

表示一条state-action-reward链

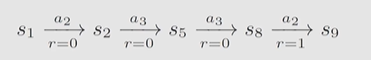
7. Return

是把沿着一条Trajectory所得到的所有reward加起来。

Discounted Return：

如果我们到达target（s9）后，策略还在不断运行，此时采取保持不动的动作（s5），Trajectory如下所示：

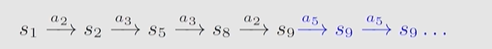
则return为：$0+0+0+1+1+1+1+…+1=\infty$，这个return会发散。

Discounted Return引入一个Discounted rate：$\gamma \in [0,1) $
$$
Discounted Return = 0+\gamma0+\gamma^20+\gamma^31+\gamma^41+\dots \
=\gamma^3(1+\gamma+\gamma^2+\dots)\
=\gamma^3(\frac{1}{1-\gamma})
$$

1. 使得return不再发散
2. 平衡更远未来和更近未来得到的reward

8. Episode

可以理解为一个包含terminal states的trajectory。

9. Markov decision process（MDP）

Key elements of MDP:

1. Sets:

   • State: the set of states $S$
   • Action: the set of actions $A$ is associated for state $s\in S$
   • Reward: the set of rewards $R(s,a)$

2. Probability distribution

   • State transition probabilty: $p(s’|s,a)$
   • Reward probability: $p(r|s,a)$

3. Policy

   $\pi(a|s)$

4. Markov property：简而言之，下一状态只和我当前的状态和选择的动作有关。

   

​ 当Policy确定时，Markov decision process就是Markov process

Bellman Equation

1. 为什么Return是重要的？

以下图为例，s1处有三种策略，哪一种是最好的？直观来说，第一个策略是最好的，因为它不会进入到forbidden area。第二种最差，第三种中间。

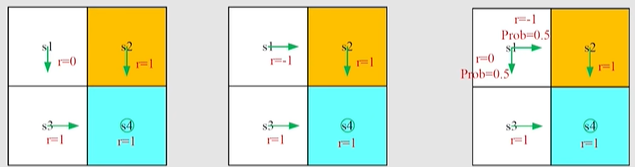
那我们能不能用数学来描述这一种直观？-答案就是：Return。它能够评估策略。
$$
return_1 = 0+\gamma1+\gamma^21+\dots = \frac{\gamma}{1-\gamma}\
return_2 = -1+\gamma1+\gamma^21+\dots = -1 + \frac{\gamma}{1-\gamma}\
return_3 = 0.5(-1 + \frac{\gamma}{1-\gamma}) + 0.5(\frac{\gamma}{1-\gamma})=-0.5+\frac{\gamma}{1-\gamma}\
$$
怎么计算Return？

上面的计算是基于return的定义。

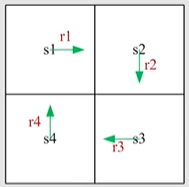
这里我们用 $v_i$ 来表示从 $s_i$ 出发的return：

$$
v_1 = r_1+\gamma r_2+\gamma^2 r_3+\dots
$$
Bootstrapping方法：从不同状态出发得到的return依赖于从其他状态得到的return：

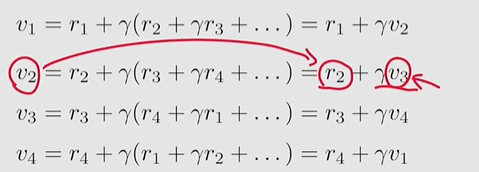
这个式子看上去很奇怪，我要得到v1就得得到v4，而得到v4又要得到v1，很矛盾，但是用矩阵的思想去解决就很简单：

上述这个式子就是Bellman Equation，但这个是针对确定性情况，对于一般情况，之后会介绍一般化的Bellman Equation。

2. State Value

首先考虑一个采取动作是 $A_t$ 的单步过程：
$$
S_t \to R_{t+1},S_{t+1}
$$
这一步中的所有的这些跳跃，都是由条件概分布决定的：

上述是一个单步的过程，可以延伸到求解一条trajectory的 discounted return ：$G_t$：
$$
G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\dots
$$
state value就是 $G_t$ 的期望值，它的计算公式是：
$$
v_\pi(s)=\mathbb{E}[G_t|S_t=s]
$$
他是一个基于状态和策略的函数，其中：

• $v(s)$ 表示从状态 $s$ 出发得到的return；
• $\pi $表示policy

3. return和state value有什么区别和联系？

return是对单个trajectory，而state value是对多个可行的trajectory得到的return求平均值。

4. Bellman Equation

如何推导Bellman equation？
$$
v_\pi(s)=\mathbb{E}[G_t|S_t=s]=\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]=\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]
$$
在状态 s 下能获得的reward的均值：
$$
\mathbb{E}[R_{t+1}|S_t=s] = \sum_a\pi(a|s)\mathbb{E}[R_{t+1}|S_t=s,A_t=a]=\sum_a\pi(a|s)\sum_r p(r|s,a)r
$$
在状态 s 下能获得的下一个状态 s’ 的return的均值：
$$
\mathbb{E}[G_{t+1}|S_t=s] = \sum_{s’}\mathbb{E}[G_{t+1}|S_{t+1}=s’]p(s’|s)=\sum_{s’}v_\pi(s’)\sum_ap(s’|s,a)\pi(a|s)
$$
最终的Bellman equation如下所示：它描述了不同状态的state value之间的关系：

它并不只是一个”式子“，如果我们有n个状态，最终我们就会有n个这样的式子，通过这n个式子我们就能把state value求解出来

5. Bellman Equation：Matrix-vector form

如何求解Bellman Equation？
$$
v_\pi(s_i)=r_\pi(s_i)+\gamma\sum_{s_j}p_\pi(s_j|s_i)v_\pi(s_j)=r_\pi+\gamma P_\pi v_\pi
$$

用矩阵向量的形式表示bellman equation的求解过程，下面有一个例子：

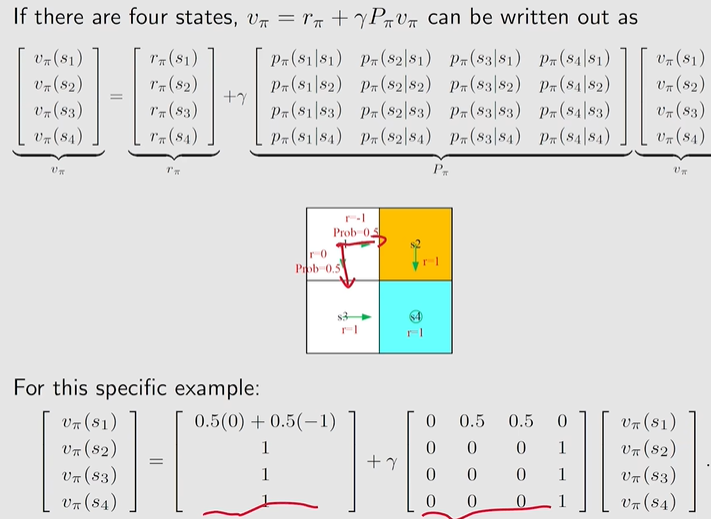
求解State Value:

为什么要求解state value？

policy evaluation：给定一个policy，求解出对应的state values叫做policy evaluation。

通过state value来评估策略的好坏，我们才能进一步改进策略，所以求解bellman equation进而求解state value是十分重要的。

怎么求解state value？

$v_\pi=r_\pi+\gamma P_\pi v_\pi \to v_\pi=(I-\gamma P_\pi)^{-1}r_\pi$，我们可以通过求逆矩阵来求解，但是在实际中，当状态空间比较大时，矩阵的维数也比较大，求逆计算量高。

在实际中我们经常用一种迭代的方法：$v_{k+1}=r_\pi+\gamma P_\pi v_k$，当$k\to\infty$时，$x_k\to v_\pi$，$v_\pi$就是真实的state value

在强化学习中，特别是对于马尔可夫决策过程（Markov Decision Process, MDP），状态值函数 ( $V(s)$ ) 的计算可以通过迭代方法来进行，这种方法称为值迭代（Value Iteration）或策略迭代（Policy Iteration）。迭代法的基本思想是逐步更新状态值，直到收敛到一个稳定的值，这比直接求解逆矩阵更高效，尤其是在状态空间较大时。

---

值迭代法

值迭代法是一种迭代算法，用于找到最优值函数 ( $V^*$ ) 和最优策略。其基本思想是反复应用Bellman方程更新每个状态的值，直到值函数收敛。

Bellman最优方程定义为：
$$
V^*(s) = \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s’} P(s’ | s, a) V^*(s’) \right]
$$

值迭代法的步骤如下：

1. 初始化值函数：
   初始化每个状态 ( $s$ ) 的值 ( $V(s)$ )，可以全部设为零或其他初始值。

2. 更新值函数：
   对每个状态 ( $s$ ) ，根据当前的值函数 ( $V(s)$ ) ，使用Bellman方程更新：
   $$
   V(s) \leftarrow \max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s’} P(s’ | s, a) V(s’) \right]
   $$

3. 检查收敛性：
   重复步骤2，直到值函数的变化小于一个预设的阈值，即：
   $$
   \max_{s} |V_{new}(s) - V_{old}(s)| < \epsilon
   $$

4. 提取最优策略：
   一旦值函数收敛，最优策略可以通过选择每个状态 ( s ) 下的最优动作 ( a ) 得到：
   $$
   \pi^*(s) = \arg\max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s’} P(s’ | s, a) V^*(s’) \right]
   $$

策略迭代法

策略迭代法通过反复执行策略评估和策略改进两个步骤来找到最优策略。

1. 策略评估：
   给定一个策略 ( $\pi$ ) ，计算其对应的值函数 ( $V^\pi(s)$ ) ，直到收敛。使用Bellman期望方程进行更新：
   $$
   V^\pi(s) = R(s, \pi(s)) + \gamma \sum_{s’} P(s’ | s, \pi(s)) V^\pi(s’)
   $$

2. 策略改进：
   给定当前的值函数 ( $V^\pi$ ) ，更新策略，使得每个状态下选择的动作最大化值函数：
   $$
   \pi_{new}(s) = \arg\max_{a \in \mathcal{A}} \left[ R(s, a) + \gamma \sum_{s’} P(s’ | s, a) V^\pi(s’) \right]
   $$

3. 重复上述步骤：
   反复执行策略评估和策略改进，直到策略不再改变，即达到最优策略。

总结：

迭代法（无论是值迭代还是策略迭代）通过逐步更新状态值或策略，最终收敛到最优解。这种方法避免了直接求解逆矩阵带来的巨大计算量，特别适用于状态空间较大的情况。

例如，值迭代法通过反复应用Bellman最优方程，逐步逼近最优值函数，而策略迭代法通过交替进行策略评估和策略改进，最终找到最优策略。这两种迭代方法在实践中广泛应用于强化学习任务中。

---

补充

Q表–FrozenLake游戏

关于Q表的实际应用，以FrozenLake这一个小游戏为例：使用ε-贪心策略选择动作 a。该策略在探索和利用之间进行权衡。

代码：

import gymnasium as gym
import numpy as np
import time

env = gym.make('FrozenLake-v1', render_mode = 'human')
s = env.reset()
env.render()

#Epsilon-Greedy approach for Exploration and Exploitation of the state-action spaces
def epsilon_greedy(Q,s,na):
    epsilon = 0.1
    p = np.random.uniform(low=0,high=1)
    if p > epsilon:
        # say here,initial policy = for each state consider the action having highest Q-value
        return np.argmax(Q[s,:])
    else:
        return env.action_space.sample()

# Q-Learning Implementation
# Initializing Q-table with zeros
Q = np.zeros([env.observation_space.n,env.action_space.n])

# set hyperparameters
lr = 0.5 #learning rate
y = 0.9 #discount factor lambda
eps = 100000 #total episodes being 100000

for i in range(eps):
    s = env.reset()[0]
    t = False
    if i % 100 == 0:
        print(f"当前迭代数：{i}")
        print(f"当前Q值表：{Q}")
    while(True):
        a = epsilon_greedy(Q,s,env.action_space.n)
        s_,r,t,_,_ = env.step(a)
        if (r==0):
            if t==True:
                r = -5 # to give negative rewards when holes turn up
                Q[s_] = np.ones(env.action_space.n)*r #in terminal state Q value equals the reward
            else:
                r = -1 # to give negative rewards to avoid long routes
        if (r==1):
                r = 100
                Q[s_] = np.ones(env.action_space.n)*r #in terminal state Q value equals the reward
        Q[s,a] = Q[s,a] + lr * (r + y*np.max(Q[s_,a]) - Q[s,a])
        s = s_
        if (t == True) :
            break

print("Q-table")
print(Q)

print("Output after learning")
#learning ends with the end of the above loop of several episodes above
#let's check how much our agent has learned
s = env.reset()
env.render()
while(True):
    a = np.argmax(Q[s[0]])
    s_,r,t,_ = env.step(a)
    print("===============")
    env.render()
    s = s_
    if(t==True) :
        break

Q-learning的更新公式

---

Q-learning的更新公式是基于贝尔曼方程（Bellman Equation），用于估计在给定状态下采取某个动作的长期回报。下面详细解释为什么Q-learning的更新公式是这样的。

1. 贝尔曼方程

贝尔曼方程描述了在某个状态下的动作价值（Q值）如何与该状态下的即时奖励和未来状态的最大Q值相关联。贝尔曼方程形式如下：
$$
Q(s, a) = \mathbb{E}[r + \gamma \max_{a’} Q(s’, a’) | s, a]
$$
其中：

• $Q(s,a)$ 是在状态 $s$ 下采取动作 $a$ 的动作价值（Q值）。
• $r$ 是即时奖励。
• $\gamma$ 是折扣因子（介于0和1之间），它决定了未来奖励在当前决策中的重要性。
• $s′$是动作 $a$ 在状态$s$ 下导致的下一个状态。
• $\max_{a’} Q(s’, a’)$是在状态$ s’ $下采取最佳动作 $a’ $的最大Q值。

Q-learning更新公式

Q-learning是一种无模型的强化学习算法，通过交互环境并更新Q表来逼近贝尔曼方程。其更新公式如下：
$$
Q(s, a) \leftarrow Q(s, a) + \alpha \left( r + \gamma \max_{a’} Q(s’, a’) - Q(s, a) \right)
$$
其中：

• $\alpha$ 是学习率，控制更新步长的大小。
• 新信息：当agent在状态 s下采取动作 a 并观察到即时奖励 r 和下一个状态 s′ 时，它获得了关于Q值的新信息，即$r + \gamma \max_{a’} Q(s’, a’)$。
• TD误差：通过计算当前Q值与新信息的差值，我们得到了时间差分（Temporal Difference，TD）误差： $\delta = r + \gamma \max_{a’} Q(s’, a’) - Q(s, a)$
• 更新Q值：使用TD误差来调整Q值： $Q(s,a)←Q(s,a)+αδ$