Llama
[TOC]
Llama
参考文章:
本文只是做一些学习记录总结,内容全部来源于以下文章和chatgpt,写的非常详细:
https://blog.csdn.net/qq_51957239/article/details/139044825
1. 模型架构
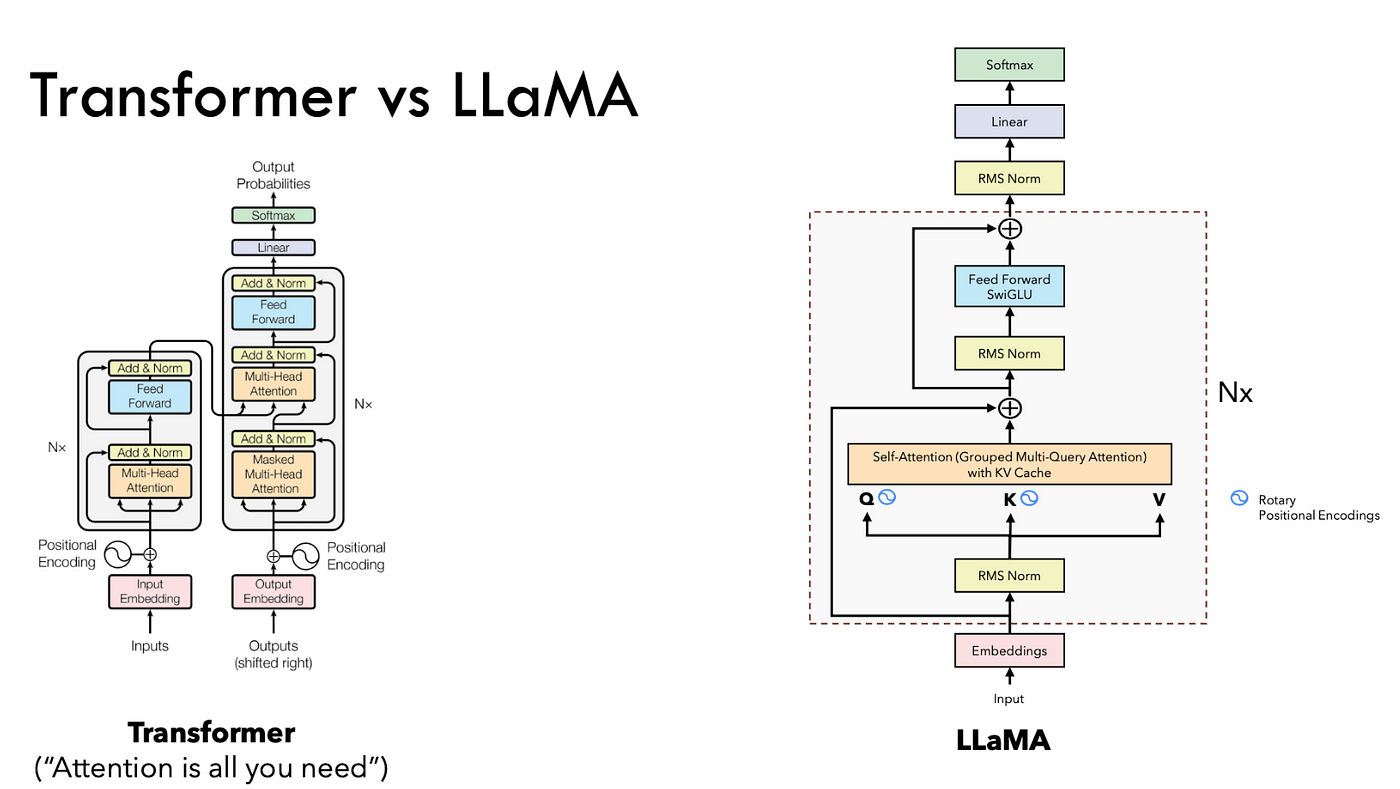
2. RMSNorm
RMSNorm(Root Mean Square Layer Normalization)是一种标准化方法,用于替代传统的 LayerNorm(Layer Normalization)。它主要是为了减少 LayerNorm 中的计算开销,同时仍能保持模型训练的稳定性和性能。相比于 LayerNorm,它省略了对均值的去除,因此计算更为简洁。
给定一个输入向量 x ,RMSNorm 的计算步骤如下:
计算 RMS 值:$\text{RMS}(x) = \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2}$;其中, $d$ 是向量的维度,$ x_i$ 是向量中的第 $ i$ 个元素。
标准化输入:$y_i = \frac{x_i}{\text{RMS}(x)}$;这是对每个输入特征进行缩放,使其除以均方根值。
缩放和偏移:通常会引入可学习的参数 $ \gamma $ 和 $ \beta $ 来进一步调整归一化后的输出:$\text{RMSNorm}(x) = \gamma y + \beta$。
位置:位置的设置应该来源于Pre-LN这个架构,具体在TransFormer那篇文章中有解释。
3. SwiGLU
SwiGLU(Switch GLU) 是一种激活函数,用于神经网络中特别是 Transformer 模型的前馈神经网络(FFN)部分。它是一种改进的激活函数,通过结合线性变换和非线性激活来提高模型的表达能力和性能。SwiGLU 是 GLU(Gated Linear Unit)激活函数的变种。
SwiGLU 公式为:
$$
\text{SwiGLU}(x) = (xW_1) \odot \text{SiLU}(xW_2)
$$
其中:
- ( $W_1$,$ W_2$ ) 是权重矩阵(通常大小为 ( $d \times 4d$ ) 和 ( $d \times 4d$ ),如果前馈层扩展到 4 倍大小)。
- ( $\text{SiLU}$ ) 是 sigmoid 线性单元激活函数,定义为:$\text{SiLU}(x) = x \sigma(x)$。其中 ( $\sigma(x)$ ) 是 sigmoid 函数。
特点:
非线性激活: SwiGLU 使用 SiLU 作为激活函数,提供了非线性变换。这比单纯的 ReLU 或 GELU 更复杂,捕捉了更多的模式和特征。
门控机制: 和 GLU 类似,SwiGLU 也具有门控机制,这使得模型能够动态地调整通道的开闭,从而更加灵活地控制信息流。
性能提升: 在一些 Transformer 变体中,SwiGLU 已被证明能够提升模型的性能,如改善模型的收敛性和表达能力。
4. RoPE
RoPE(Rotary Position Embedding) 是一种位置编码方法,用于在 Transformer 模型中表示序列数据的位置信息。与传统的绝对位置编码(例如,正弦-余弦位置编码)不同,RoPE 提供了一种相对位置编码的方式,使模型能够更好地捕捉序列数据中相对位置的重要性。
$$
\text{RoPE}(x_i) = x_i \cos(\Theta_i) + \text{Rotate}(x_i, \sin(\Theta_i))
$$
RoPE 的核心思想
RoPE 的核心思想是通过旋转输入的词嵌入来引入位置信息。具体来说,RoPE 将输入向量根据其位置应用一个旋转矩阵,这个旋转矩阵的旋转角度依赖于该位置。
公式解析
- 输入向量 $x_i$
$x_i$ 是第 $i$ 个位置的输入向量,通常是从词嵌入或某一层神经网络的输出中得到的。这是一个长度为 $d$ 的向量,其中 $ d$ 是模型的嵌入维度。
- 旋转角度 $\Theta_i $
$ \Theta_i$ 是与位置 $ i$ 相关的旋转角度。这个角度由位置编码生成,与正弦/余弦位置编码类似,RoPE也会根据位置生成一组旋转角度。
- 旋转操作的两个部分
第一个部分:$x_i \cos(\Theta_i) $
这是对向量 $x_i$ 的每个分量与对应的旋转角度的余弦值相乘。这个操作类似于在旋转变换中保持部分原有的向量信息。
第二个部分: $\text{Rotate}(x_i, \sin(\Theta_i)) $
这是对向量 $x_i $ 进行旋转。具体来说,这是将向量 $x_i$ 的各分量与相应的旋转角度的正弦值相乘,然后进行旋转。这部分通常涉及在向量的每对相邻分量之间进行变换,如在二维空间中,点 (x, y) 的旋转可以表示为 (-y, x) 。在高维空间中,这个操作是对每一对分量进行类似的旋转变换。
计算过程
为了更清楚地理解计算过程,我们以一个二维向量 $x_i = (x, y) $ 为例,旋转角度为 $\Theta_i $。实际操作中,我们需要为每对相邻分量执行以下计算:
计算余弦部分:对应的旋转余弦部分是:$(x \cos(\Theta_i), y \cos(\Theta_i))$
计算正弦旋转部分:对应的旋转正弦部分是:$(-y \sin(\Theta_i), x \sin(\Theta_i))$
组合结果:最终结果是将上述两部分相加:$(x \cos(\Theta_i) - y \sin(\Theta_i), y \cos(\Theta_i) + x \sin(\Theta_i))$
在更高维度中,这个过程类似,但会应用到每一对相邻的向量分量。通过这种方式,每个位置向量 $ x_i $ 都被旋转了一个位置相关的角度,这种旋转操作使得位置编码不再是静态的(即固定不变),而是能够自然地包含序列中元素的相对位置信息。
我的困惑–然后GPT给出的回答
问题:
比如现在有token_1和token_2
正弦/余弦位置编码的点积表示了一种相对位置信息,这个信息不就是向量之间的距离吗?我认为这和RoPE的点积很相似啊,RoPE的点积结果不是代表了角度吗?而正弦/余弦位置编码的点积代表了位置的距离,这有什么需要模型学习解码的?
回答:
正弦/余弦位置编码和RoPE两者的点积的确都反映了位置之间的一种关系,但它们提供的位置信息形式和模型利用这些信息的方式有所不同。
正弦/余弦位置编码中的点积
在正弦/余弦位置编码中,每个位置 (i) 的编码是一个固定的向量,这个向量的各个分量是正弦和余弦函数的值,基于位置 (i) 的绝对值和编码维度进行计算。
点积结果解释:
点积结果的大小不仅仅是向量之间的“距离”,而是两向量之间的夹角的余弦值,这个夹角与位置编码向量在高维空间中的关系有关。这种关系在某种程度上反映了相对位置信息,但模型需要通过训练过程学习如何将这种点积结果与序列中元素的实际关系联系起来。换句话说,模型必须“学习解码”这种高维向量空间中的角度信息,以便在特征表达中有效地捕捉位置之间的相对关系。
RoPE中的点积
RoPE通过旋转操作为每个位置引入了一个与位置相关的角度,旋转后的向量编码了相对位置信息。对于两个位置 (i) 和 (j),经过RoPE处理后的向量的点积会直接反映这两个位置之间的相对角度差异。由于旋转角度与位置差异直接相关,因此点积结果自然包含了这种相对位置信息。
点积结果解释:
在RoPE中,这个点积结果更明确地表示了位置之间的角度差,而不是正弦/余弦位置编码中那种隐含的相似性。由于RoPE通过旋转方式使得相对位置信息显式存在,这种信息的解码变得更直接,不需要模型去学习如何从复杂的高维空间向量关系中提取相对位置。
总结和比较
正弦/余弦位置编码:点积结果隐含了位置之间的相对距离信息,但这种信息是以复杂的高维空间关系的形式存在的。模型需要在训练过程中学习如何解码这种关系,将点积结果与实际的相对位置信息关联起来。
RoPE:点积结果直接反映了位置之间的相对角度差异,信息更明确且容易解码。模型能够更直观地利用这些信息来理解序列中元素之间的相对位置关系。
5. GQA
在理解什么是GQA之前,我们还需要知道两个概念:MHA和MQA,下图展示了MHA,MQA,GQA的区别:
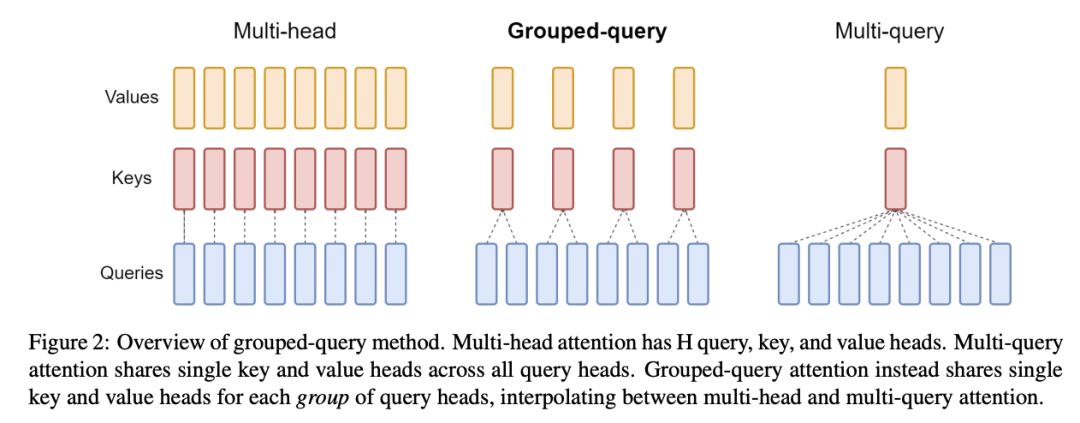
MHA:
MHA(Multi-Head Attention):多头注意力机制,将输入数据分成多个头(heads),这些头通常具有不同的权重矩阵,因此可以关注输入序列中的不同部分和特征。每个头独立地执行注意力计算。每次做 Attention,不同head的 Q、K、V 就做好自己运算就可以,输出时各个head的输出结果加起来就行。
MQA:
MQA(Multi-Query Attention):多查询注意力机制,MQA的原理很简单,简单来说Q仍然是多头,K,V是共享的。它将原生Transformer每一层多头注意力的Key线性映射矩阵、Value线性映射矩阵改为该层下所有头共享,也就是说K、V矩阵每层只有一个。
举例来说,以ChatGLM2-6B为例,一共28层,32个注意力头,输入维度从4096经过Q、K、V矩阵映射维度为128,若采用原生多头注意力机制,则Q、K、V矩阵各有28×32个,而采用MQA的方式则整个模型包含28×32个Q矩阵,28×1个K矩阵,28×1个V矩阵。这种方法在提高推理效率的同时,也能够保持模型的性能。
GQA:
MQA虽然能最大程度减少KV Cache所需的缓存空间,但是可想而知参数的减少意味着精度的下降,所以为了在精度和计算之间做一个trade-off,GQA (Group Query Attention)应运而生,即Q依然是多头,但是分组共享K,V,既减少了K,V缓存所需的缓存空间,也暴露了大部分参数不至于精度损失严重。
KV Cache:
大模型推理性能优化的一个常用技术是KV Cache。
在自回归生成任务中,模型需要逐个生成序列中的tokens,每次生成一个新token时,都会更新输入序列并重新计算自注意力。然而,已生成的部分(历史tokens)对应的Key和Value向量在生成后续token时往往保持不变或变化较小。KV Cache正是利用了这一性质,通过将这些历史tokens对应的Key和Value向量存储起来(缓存),在后续计算中直接复用,而不是每次都重新计算。
6. BPE–Sentence piece
7. MoE结构
MoE(Mixture-of-Experts)是一种深度学习中的架构,旨在提高模型的性能和效率,尤其在处理大规模数据时表现优越。MoE结构通过将任务分配给多个专家模型(子模型)来实现。这些专家模型通常具有不同的能力或特长,而最终的输出是由一个门控网络(gating network)根据输入数据动态选择的。
MoE的基本组成部分:
专家模型(Experts):
这些是多个并行的子模型,每个模型都有自己特定的参数集和能力。
专家模型的结构可以是全连接层、卷积神经网络、Transformer等多种类型,具体取决于任务和数据的需求。
门控网络(Gating Network):
门控网络的任务是根据输入数据的特征,动态地为每个输入样本选择最合适的专家模型。
它通常输出一个概率分布,这些概率值表示每个专家模型的重要性或选择的权重。
在前向传播时,只有少数几个专家模型会被激活(参与计算),以减少计算资源的使用。
组合机制:
门控网络计算出的权重用于加权求和专家模型的输出,形成最终的模型输出。
这种组合可以是简单的加权和,也可以是更复杂的操作,取决于具体的应用场景。
MoE的优势:
计算效率:
由于每次只有一部分专家模型被激活,MoE结构可以显著减少计算开销,尤其适用于大型模型。
模型容量:
通过并行多个专家模型,MoE可以在不显著增加计算资源的情况下增加模型的表示能力。
适应性和灵活性:
门控网络可以根据输入数据选择不同的专家模型,使得MoE在处理多样化和复杂数据时表现更好。
应用场景:
MoE结构在许多领域有广泛应用,包括自然语言处理、计算机视觉和推荐系统等。在这些应用中,MoE通常用于处理大规模数据集,并且能够适应数据的多样性。