RT-DETR

[TOC]

RT-DETR

本篇是对以下文章的学习记录：

https://blog.csdn.net/weixin_43694096/article/details/133183315

https://zhuanlan.zhihu.com/p/626659049

模型结构

结构：Backbone+Neck+Head

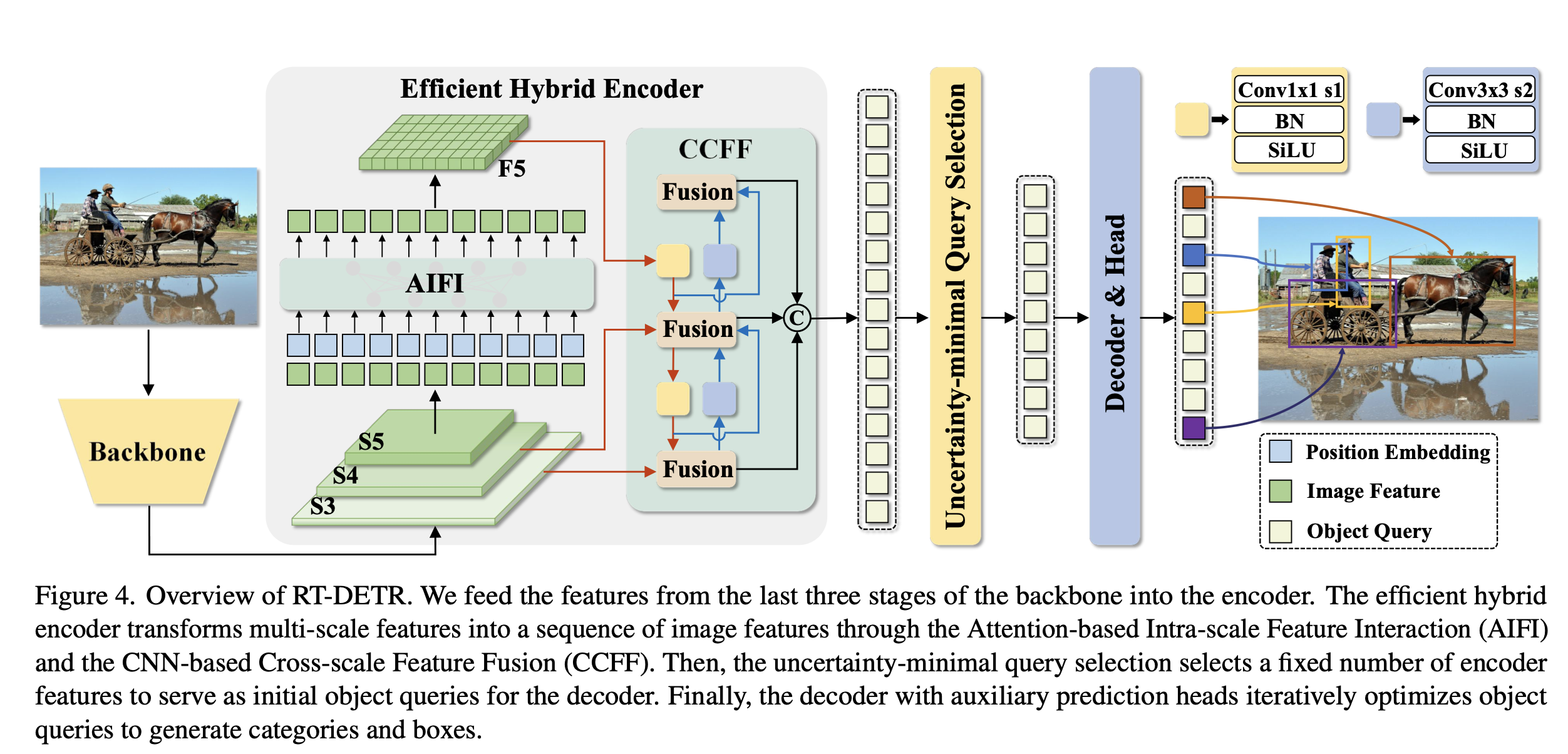
Backbone

---

对于Backbone部分，采用了经典的 Resnet和可缩放的 HgnetV2两种，两种 backbone各训练了两个版本。

以HgnetV2为Backbone的RT-DETR包括L和X版本，Hgnetv2是由百度自家研发的主干结构。

以ResNet为Backbone的RT-DETR则包括RT-DETR-R50和RT-DETR-R101

与YOLO相似的地方在于，RT-DETR最终会输出三种不同尺寸的特征图，它们相对于输入图像的分辨率下采样倍数分别是8倍、16倍和32倍。这与主流的YOLO算法相似。除此之外,在主干结构的其他方面，RT-DETR并没有特别的地方。

Neck–Efficient Hybrid Encoder

---

对于Neck部分，RT-DETR采用了高效混合编码器。

通过基于注意力的尺度内特征交互AIFI和跨尺度特征融合模块CCFF，将多尺度特征图转为图像特征序列。

• AIFI「Attention-based Intra-scale Feature Interaction」

  其实他就是一个很普通的Transformer的Encoder层，包含标准的MSAH（多头自注意力机制或者Deformable Attention）和FFN前馈网络。

  RT-DETR只将Encoder作用在 S5 特征上，文章解释是出于两点考虑：

  1. 以往的DETR，如Deformable DETR是将多尺度的特征都拉平成拼接在其中，构成一个序列很长的向量，尽管这可以使得多尺度之间的特征进行充分的交互，但也会造成极大的计算量和计算耗时。RT-DETR认为这是当前的DETR计算速度慢的主要原因之一；
  2. RT-DETR认为相较于较浅的S3特征和S4特征，S5特征拥有更深、更高级、更丰富的语义特征，这些语义特征是Transformer更加感兴趣的和需要的，对于区分不同物体的特征是更加有用的，而浅层特征因缺少较好的语义特征而起不到什么作用。

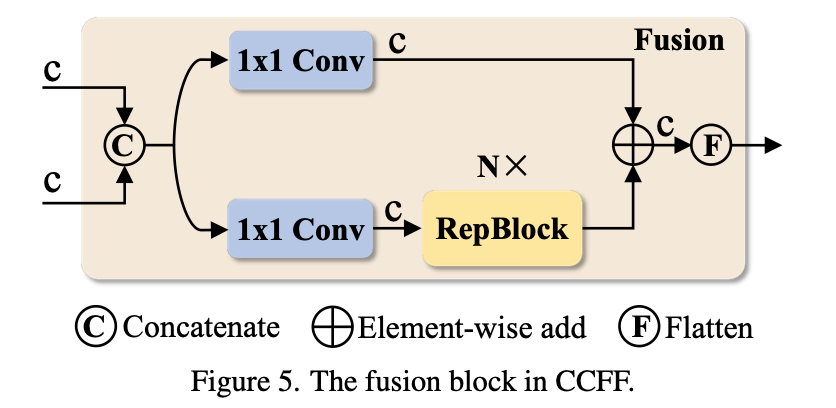
• CCFF「CNN-based Cross-scale Feature-fusion」

  CCFF模块，以YOLO的角度看这个结构的话，这个CCFF模块就是一个PA-FPN结构。

  关于CCFF模块中的 Fusion，是由2个1×1卷积和N个 Repblock构成的，这里之所以写成N，我觉得是因为RTDETR可以进行缩放处理，通过调整CCFM中 Repblock的数量和 Encoder的编码维度分别控制 Hybrid Encoder的深度和宽度，同时对 backbone进行相应的调整即可实现检测器的缩放。

  

IoU-aware Query Section

---

使用”**IoU感知查询选择”**从Encoder输出的特征序列中选择固定数量的特征作为object queries。其经过Decoder后由预测头映射为置信度和边界框。

问题：

1. 现有的DETR变体都是利用这些特征的分类分数直接选择Top-K特征。然而，由于分类分数和IoU分数的分布存在不一致，分类得分高的预测框并不一定是和GT最接近的框，这导致高分类分数+低IoU分数的框会被选中，而低分类分数+高IoU分数的框会被丢弃，这将会损害检测器的性能。
2. 换一种说法，在传统的目标检测训练中，每个目标的类别标签通常是通过one-hot编码来表示的，即对于一个特定的类别，对应的标签向量中只有一个元素是1，其余元素都是0。这种方式的一个潜在问题是，它可能允许分类任务过早地收敛，即使目标的定位（即边界框的位置和大小）还不够准确。

解决：

“IoU-aware”的概念被引入到目标检测的训练中。具体来说，模型的分类损失会考虑到预测边界框与真实边界框之间的IoU。

在”IoU-aware”的训练策略中，只有当预测边界框与真实边界框的IoU超过某个阈值时，模型才会将该目标的类别标签视为正确的分类。
它迫使模型在进行分类预测之前，必须先准确地定位目标。因为如果边界框定位不准确，即使类别预测正确，由于IoU较低，模型仍然会收到较高的分类损失，从而鼓励模型同时优化分类和定位任务。这样可以提高模型的整体性能，尤其是在需要精确边界框定位的任务中。

简而言之，通过在训练期间约束检测器对高IoU的特征产生高分类分数，对低IoU的特征产生低分类分数。从而使得模型根据分类分数选择的Top-K个特征对应的预测框同时具有高分类分数和高IoU分数。

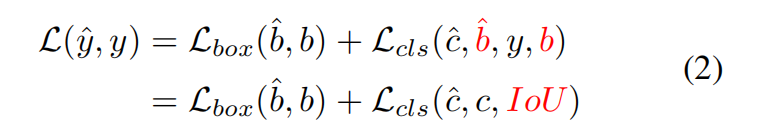
其中，$\hat{y}$ 和 $y$ 分别表示预测和真实值，$\hat{y}=({\hat{c},\hat{b}})$和$y = ({c, b})$，$c$ 和 $b$分别表示类别和边界框。我们将IoU分数引入到分类分支的损失函数中，以实现对正样本的分类和定位的一致性约束。

效果：

文中通过可视化这些编码器特征的置信度分数以及和GT之间的IoU分数之后发现，IoU-aware Query Section明显提高了被选中的特征的质量。

Decoder

---

Q（Queries）、K（Keys）、V（Values）

Q是由经过IoU-Aware Query Selection模块筛选后的Object Queries生成的。这些查询向量代表了检测器将要预测的目标位置和类别的“槽位”。这些Object Queries作为解码器的输入，经过一系列线性变换得到Q矩阵。

K 和V通常是从编码器输出的图像特征中生成的。在RT-DETR中，编码器部分处理输入图像，生成特征图。这些特征图通过线性变换分别生成K和V。

在DETR（Detection Transformers）模型的原始设计中，Decoder部分使用的是cross attention，也称为交叉注意力机制。

在一些DETR的后续改进版本中（如DINO、Deformable DETR等），引入了deformable attention机制。

deformable attention是一种变体注意力机制，旨在解决标准cross attention计算复杂度高的问题。它的工作原理是：

1. 局部感知：不像标准的cross attention在全局特征图上操作，deformable attention只在特定的采样位置上操作。这些采样位置是通过学习得到的，可以针对每个查询自适应地确定。
2. 稀疏计算：由于只在少量位置上计算注意力，deformable attention大大降低了计算复杂度，尤其在处理高分辨率特征图时。

LOSS

在训练的loss上，回归损失还是GIoU损失和L1损失，而类别损失上引入“IoU软标签”

分类损失：IoU 软标签

在 RT-DETR 中，类别损失引入了“IoU 软标签”，这种设计的目的是更好地反映预测框和真实框之间的重叠程度，从而在训练过程中提供更准确的梯度信息。

什么是 IoU 软标签？

IoU 软标签是一种将 IoU 值作为目标类别的软标签（soft label）的策略。具体来说，对于每个预测框，其类别标签不再是一个二元变量（0 或 1），而是一个反映预测框与真实框 IoU 的值。

IoU 软标签的计算

假设有 ($C$) 个类别，对于每个预测框 ($i$) 和类别 ($c$)，其 IoU 软标签定义为：
$$
t_i^c = \text{IoU}(\text{pred}_i, \text{gt}_i^c)
$$

其中 ($\text{pred}_i$) 是第 ($i$) 个预测框，($\text{gt}_i^c$) 是第 ($i$) 个真实框，$t_i^c$在类别 ($c$) 下的 IoU。

IoU 软标签的损失计算

类别损失通常使用交叉熵损失，但在 RT-DETR 中，使用了 IoU 软标签的变体：
$$
\mathcal{L}_{\text{cls}} = -\sum_i \sum_c t_i^c \log(p_i^c)
$$
其中 ( $p_i^c$ ) 是预测框 ($i$) 属于类别 ($c$) 的概率。

回归损失：GIoU 和 L1 损失

Generalized IoU (GIoU) 损失

GIoU 是一种改进的 IoU 损失，解决了 IoU 损失在没有重叠的情况下梯度为零的问题。GIoU 损失的公式如下：
$$
\text{GIoU} = \text{IoU} - \frac{|\text{C} - \text{U}|}{|\text{C}|}其中：
$$

• ($\text{IoU}$) 是交并比（Intersection over Union）。
• ($\text{C}$) 是包围预测框和真实框的最小闭包区域的面积。
• ($\text{U}$) 是预测框和真实框的并集面积。

GIoU 损失则定义为：
$$
\text{GIoU Loss} = 1 - \text{GIoU}
$$
L1 损失

L1 损失（也称为绝对误差损失）用于衡量预测框和真实框的坐标之间的绝对差异：
$$
\text{L1 Loss} = \sum_{i \in {x, y, w, h}} |p_i - t_i|
$$

其中 ( $p_i$ ) 是预测框的坐标， ( $t_i$ ) 是真实框的坐标。

在 RT-DETR 中，回归损失是 GIoU 损失和 L1 损失的加权和：
$$
\mathcal{L}_{\text{reg}} = \lambda_1 \cdot \text{GIoU Loss} + \lambda_2 \cdot \text{L1 Loss}
$$

其中 ($\lambda_1$) 和 ($\lambda_2$) 是权重系数。

综合损失

RT-DETR 的综合损失函数是回归损失和类别损失的加权和：
$$
\mathcal{L} = \mathcal L_{reg} + \mathcal L_{cls}
$$

总结

RT-DETR 在训练过程中通过结合 GIoU 损失和 L1 损失来优化边界框回归，同时引入 IoU 软标签用于类别损失。这种设计使得模型能够更精确地处理边界框位置和类别分类，从而提高检测性能。

Deformable attention

RepVGG

RepVGG 是一种通过重参数化（Re-parameterization）技术实现的卷积神经网络架构。它在训练和推理阶段使用不同的网络结构，以同时获得训练时的高表达能力和推理时的高效率。RepVGG的设计灵感来自于经典的VGG网络，强调简单的架构设计，但通过重参数化技术实现了更高的推理速度。

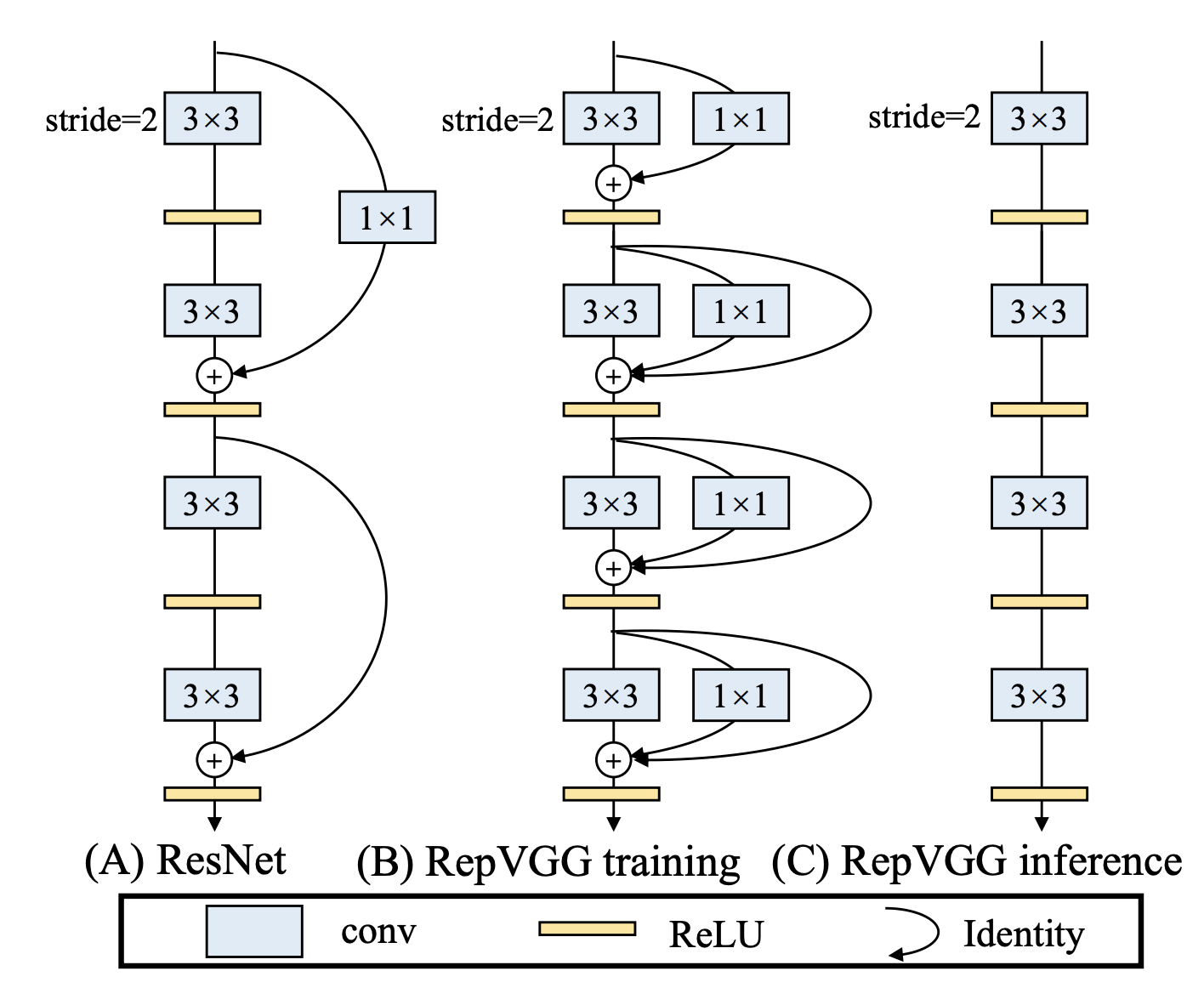
核心思想：

在训练阶段，使用一个复杂的网络结构，通过多分支卷积层捕获丰富的特征；

在推理阶段，将这些分支融合成一个单独的卷积层，从而简化计算并加速推理。

重参数化具体过程：

RepVGG 中的重参数化技术是指将训练阶段的多分支卷积结构在推理阶段重新参数化为一个单一的等效卷积层。

1. 训练阶段

   主分支：通常是一个标准的3x3卷积，用于捕捉局部特征。

   辅助分支：可能包括1x1卷积、3x3卷积，甚至是恒等映射（identity mapping）。这些分支有助于学习不同的特征表示，并增加模型的表达能力。

   在训练阶段，这些分支的输出会被合并（例如通过逐元素相加），以形成最终的特征输出。这种多分支结构使得网络可以学习到更丰富的特征，从而提升模型性能。

2. 推理阶段

   在推理阶段，执行多分支操作会增加计算开销和延迟。因此，在推理阶段，RepVGG将这些分支通过重参数化技术合并为一个等效的单一卷积层，从而大大简化了计算。具体来说，这一过程涉及以下步骤：

   权重合并：对于所有的卷积分支，它们的权重矩阵可以被合并成一个新的卷积核。例如，假设有一个3x3卷积和一个1x1卷积，可以通过将1x1卷积的权重嵌入到一个等效的3x3卷积核中，来实现等效的计算。

   偏置合并：每个分支的偏置项也会被合并为一个单一的偏置值。

   恒等映射的处理：对于恒等映射分支（如Residual连接），它们可以通过添加到卷积的偏置中来处理。

例子：

要将1x1卷积的效果嵌入到3x3卷积中，我们可以将1x1卷积的权重扩展到3x3的空间维度。具体步骤如下：

对于1x1卷积的每个通道，我们在3x3卷积核的中心位置设置对应的权重值，其余位置设置为零。这样可以确保原来1x1卷积的作用在合并后的3x3卷积中仍然存在。这可以表示为：
$$
W{\prime}{3x3}[c{out}, c_{in}, i, j] =
\begin{cases}
W_{1x1}[c_{out}, c_{in}, 0, 0] & \text{if } i = j = 1 \
0 & \text{otherwise}
\end{cases}
$$

其中 $i$, $j$ 是3x3卷积核的空间坐标， $c_{out}$ 和 $c_{in}$ 分别是输出和输入通道的索引。

偏置项的合并相对简单。合并后的等效卷积层的偏置项 $b{\prime}$ 直接等于原来各个分支的偏置项之和：
$$
b{\prime} = b_{3x3} + b_{1x1}
$$
最终的等效3x3卷积的权重 $W_{3x3}^{\text{final}}$ 是主分支的3x3卷积权重 $W_{3x3}$ 和从1x1卷积嵌入的权重 $W^{\prime}_{3x3}$的叠加：

$$
W_{3x3}^{\text{final}} = W_{3x3} + W{\prime}_{3x3}
$$
优势：

• 高效推理：通过重参数化，RepVGG 在推理时只需执行标准的卷积操作，而不需要额外的分支计算，因此推理速度更快。
• 高表达能力：在训练阶段，通过多个分支捕捉不同的特征模式，提高了模型的表达能力。
• 简单结构：最终的推理模型结构非常简单，没有复杂的分支或跳跃连接，易于实现和优化。

缩放

在深度学习中，缩放（scaling） 通常指的是对神经网络的架构进行调整，以适应不同的计算资源和应用需求。这种调整可以涉及网络的深度（depth）、宽度（width）、以及输入分辨率。在RT-DETR中的CCFM模块和Hybrid Encoder中，通过调整RepBlock的数量和编码维度来控制网络的深度和宽度，这种操作就属于模型的缩放。

• 控制深度：深度通常指网络中的层数。

  在RT-DETR中，CCFM模块中RepBlock的数量决定了该模块的深度。增加RepBlock的数量，相当于增加了网络的深度，使得模型能够捕捉到更复杂的特征和更深层次的信息。然而，增加深度也会带来更多的计算和存储开销。因此，通过调整RepBlock的数量，可以在计算资源和模型性能之间进行平衡。

• 控制宽度：宽度通常指每一层中的通道数，即每一层的特征图的深度。

  在RT-DETR中的Hybrid Encoder中，编码维度决定了模型的宽度。增加编码维度可以增加每一层特征图的通道数，使得模型能够容纳更多的特征表示。宽度的增加通常会带来更丰富的特征表达能力，但也会增加计算和存储开销。

• 模型缩放的意义

  1. 灵活适应计算资源：通过调整模型的深度和宽度，可以在不同的硬件环境下灵活适应。例如，在资源充足的服务器上，可以使用更深、更宽的模型来提高精度；在计算资源有限的移动设备上，可以使用较浅、较窄的模型来保证实时性。

  2. 平衡性能与效率：模型缩放可以帮助在模型性能和推理速度之间找到最佳平衡点。例如，在实时目标检测任务中，可能需要在一定的精度损失下，优先确保推理速度。

  3. 网络结构的可扩展性：通过缩放机制，可以方便地创建多个版本的模型，以适应不同的任务需求。例如，一个任务可能需要更高的检测精度，而另一个任务可能对速度要求更高。